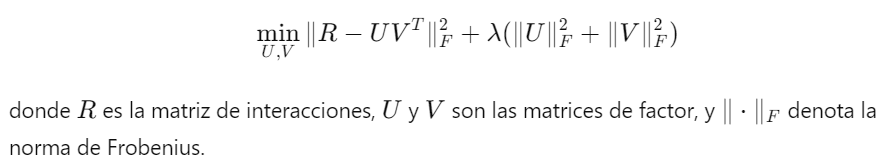Técnicas Avanzadas de Regularización
La regularización es una técnica fundamental en el aprendizaje automático para prevenir el sobreajuste y mejorar la generalización de los modelos. Más allá de las técnicas clásicas como L1 y L2, existen métodos avanzados de regularización que se adaptan a problemas más específicos y complejos. En este texto, exploraremos tres técnicas avanzadas de regularización: Regularización de Grupo (Group Lasso), Regularización de Matrices (Matrix Regularization) y Regularización Bayesiana, explicando sus aplicaciones y ventajas.
Regularización de Grupo (Group Lasso)
Aplicación a la Selección de Grupos de Variables
Group Lasso es una extensión de la regularización Lasso que se utiliza para la selección de grupos de variables en lugar de variables individuales. Este método es especialmente útil cuando las variables están naturalmente agrupadas, y se desea seleccionar o eliminar grupos completos en lugar de variables individuales.
1. Descripción del Método: En Group Lasso, las variables se agrupan en conjuntos, y se aplica una penalización a la suma de las normas L2 de los coeficientes dentro de cada grupo. La función de costo para Group Lasso se define como:
donde βg es el vector de coeficientes del grupo g y λ es el parámetro de regularización.
- Selección de Grupos: Permite seleccionar grupos completos de variables, lo cual es beneficioso cuando las variables dentro de un grupo están altamente correlacionadas.
- Interpretabilidad: Facilita la interpretabilidad del modelo al mantener o eliminar grupos completos de características.
3. Aplicaciones: Group Lasso es útil en aplicaciones donde las variables están organizadas en grupos, como en el análisis de imágenes, genómica y señales de tiempo.
Regularización de Matrices (Matrix Regularization)
Aplicación en Problemas de Recomendación y Factorización de Matrices
La regularización de matrices se utiliza en problemas donde los datos pueden representarse en forma de matrices, como en sistemas de recomendación y factorización de matrices.
1. Descripción del Método: En problemas de recomendación, se busca factorizar una matriz de interacciones (por ejemplo, usuarios y productos) en dos matrices de menor rango. La regularización se aplica para evitar el sobreajuste y mejorar la generalización de la factorización.
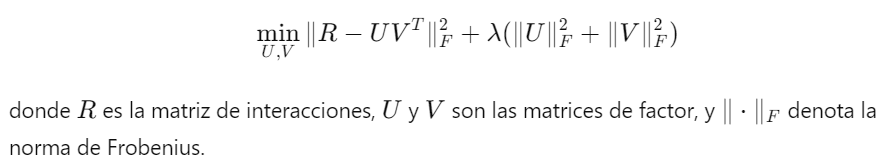
2. Ventajas:
- Reducción de la Complejidad: La regularización ayuda a evitar que las matrices factorizadas capturen demasiado ruido en los datos.
- Mejora de la Generalización: Al controlar la magnitud de los valores en las matrices factorizadas, se mejora la capacidad del modelo para generalizar a nuevos datos.
3. Aplicaciones: La regularización de matrices es ampliamente utilizada en sistemas de recomendación, como la recomendación de productos en plataformas de comercio electrónico y servicios de streaming.
Regularización Bayesiana
Enfoques Bayesianos para la Regularización
La regularización bayesiana introduce una perspectiva probabilística al problema de la regularización, incorporando conocimientos previos en la modelización.
1. Descripción del Método: En la regularización bayesiana, los parámetros del modelo se tratan como variables aleatorias y se definen distribuciones previas sobre ellos. La inferencia se realiza mediante la combinación de la información de los datos (verosimilitud) con la información previa (prior), resultando en la distribución posterior.
2. Comparación con Métodos Frecuentistas:
- Flexibilidad: Los métodos bayesianos permiten la incorporación explícita de conocimientos previos, lo que puede ser ventajoso en situaciones con datos limitados.
- Inferencia Completa: Proporcionan una distribución completa sobre los parámetros, permitiendo una evaluación más rica de la incertidumbre.
- Computacionalmente Intensivo: Los enfoques bayesianos pueden ser más complejos y requerir técnicas de muestreo como MCMC (Markov Chain Monte Carlo) para la inferencia.
3. Aplicaciones: La regularización bayesiana es utilizada en diversas áreas, incluyendo la estimación de modelos con datos escasos, la detección de anomalías y la modelización predictiva con altos niveles de incertidumbre.
En resumen, las técnicas avanzadas de regularización, como Group Lasso, la regularización de matrices y la regularización bayesiana, ofrecen poderosas herramientas para mejorar la generalización de los modelos de aprendizaje automático y prevenir el sobreajuste. Cada técnica se adapta a diferentes contextos y problemas específicos, proporcionando flexibilidad y robustez en la construcción de modelos predictivos precisos y confiables.Enlace Adicional
Para más información, visite este sitio.
Campus
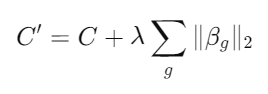donde es el vector de coeficientes del grupo y es el parámetro de regularización.
Campus
