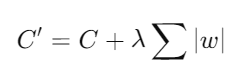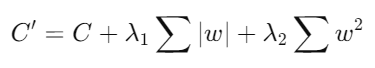Regularización y Selección de Variables
En el contexto del aprendizaje automático y la estadística, la regularización y la selección de variables son técnicas fundamentales para manejar modelos de alta dimensión. En modelos con un gran número de variables, es crucial seleccionar las más relevantes para mejorar la interpretabilidad y el rendimiento del modelo. La regularización ayuda a prevenir el sobreajuste y facilita la selección de variables de manera integrada. Este texto explorará la importancia de la selección de variables, los métodos de selección de variables integrados con regularización y las técnicas de reducción de dimensionalidad como regularización implícita.
Importancia de la Selección de Variables en Modelos de Alta Dimensión
En modelos con un gran número de variables, es común que muchas de ellas sean irrelevantes o redundantes. Incluir estas variables innecesarias puede llevar a problemas como el sobreajuste, donde el modelo aprende el ruido en los datos en lugar de los patrones subyacentes. La selección de variables es crucial por varias razones:
1. Mejora de la Interpretabilidad: Reducir el número de variables facilita la comprensión del modelo y su interpretación, lo que es especialmente importante en aplicaciones donde la explicabilidad es crucial.
2. Reducción de la Varianza: Eliminar variables irrelevantes puede reducir la varianza del modelo, mejorando su capacidad de generalización a nuevos datos.
3. Eficiencia Computacional: Trabajar con un menor número de variables reduce los requisitos computacionales, lo que es beneficioso para el entrenamiento y la implementación del modelo.
Métodos de Selección de Variables Integrados con Regularización
Los métodos de selección de variables integrados con regularización combinan la penalización de la complejidad del modelo con la eliminación de variables irrelevantes. Algunos de los métodos más comunes incluyen:
1. Lasso (Least Absolute Shrinkage and Selection Operator)
- Descripción: Lasso añade una penalización L1 a la función de costo del modelo, lo que fuerza a que algunos coeficientes se reduzcan exactamente a cero, eliminando así variables irrelevantes.
donde C es la función de costo original, λ es el parámetro de regularización, y w son los coeficientes del modelo.
- Ventajas: Lasso realiza automáticamente la selección de variables y puede manejar grandes conjuntos de datos de manera eficiente.
- Descripción: Elastic Net combina las penalizaciones L1 y L2, proporcionando un balance entre la selección de variables de Lasso y la regularización de Ridge.
- Ventajas: Elastic Net es útil cuando hay correlación entre variables, ya que puede seleccionar grupos de variables correlacionadas en lugar de eliminar una sola variable de cada grupo.
Técnicas de Reducción de Dimensionalidad como Regularización Implícita
Las técnicas de reducción de dimensionalidad también actúan como una forma de regularización implícita al transformar los datos en un espacio de menor dimensión, manteniendo las características más importantes. Algunas de estas técnicas incluyen:
1. Análisis de Componentes Principales (PCA)
- Descripción: PCA transforma los datos originales en un nuevo conjunto de variables no correlacionadas llamadas componentes principales. Estas componentes son combinaciones lineales de las variables originales y están ordenadas por la cantidad de varianza que explican en los datos.
- Ventajas: PCA reduce la dimensionalidad de los datos y puede mejorar el rendimiento del modelo al eliminar el ruido y las redundancias.
2. Análisis de Componentes Independientes (ICA)
- Descripción: ICA busca encontrar componentes independientes en los datos que maximicen la independencia estadística. Es útil en aplicaciones donde las fuentes de los datos son independientes.
- Ventajas: ICA es particularmente útil para el análisis de señales y puede descomponer datos complejos en componentes más interpretables.
En resumen, la selección de variables y la regularización son técnicas cruciales en el manejo de modelos de alta dimensión. La integración de métodos de regularización como Lasso y Elastic Net permite la selección automática de variables, mejorando la interpretabilidad y el rendimiento del modelo. Además, las técnicas de reducción de dimensionalidad como PCA e ICA actúan como formas de regularización implícita, ayudando a reducir la complejidad del modelo y mejorar su capacidad de generalización. Estas estrategias son esenciales para desarrollar modelos robustos y eficientes en el análisis de datos y el aprendizaje automático.
 Campus
Campus