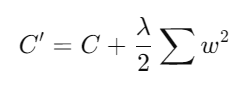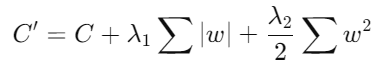Regularización en el Contexto de Datos de Alta Dimensión
En el análisis de datos y el aprendizaje automático, los datos de alta dimensión presentan desafíos únicos que pueden complicar el proceso de modelado y aumentar el riesgo de sobreajuste (overfitting). La regularización se vuelve especialmente crucial en este contexto para mejorar la capacidad de generalización de los modelos. En este texto, exploraremos los desafíos específicos de los datos de alta dimensión, las adaptaciones y consideraciones para la regularización, y las técnicas específicas para manejar estos datos.
Desafíos Específicos de los Datos de Alta Dimensión
1. Mal de la Dimensionalidad: A medida que aumenta el número de dimensiones (características), el espacio de características se vuelve exponencialmente grande, haciendo que los datos se dispersen. Esto dificulta la detección de patrones significativos y puede conducir a un rendimiento deficiente del modelo.
2. Sobreajuste: Con muchos más parámetros que ejemplos, los modelos pueden aprender ruido en lugar de patrones subyacentes, lo que resulta en un alto riesgo de sobreajuste. Los modelos complejos tienden a ajustarse demasiado a los datos de entrenamiento, capturando detalles específicos y fallando en generalizar.
3. Cálculo y Almacenamiento: Los datos de alta dimensión requieren mayor capacidad de almacenamiento y potencia computacional, lo que puede hacer que el entrenamiento y la implementación del modelo sean más costosos y lentos. Adaptaciones y Consideraciones para la Regularización
1. Penalización de la Magnitud de los Pesos: En datos de alta dimensión, es crucial limitar la magnitud de los pesos para evitar modelos demasiado complejos. Las técnicas como la regularización L1 y L2 ayudan a controlar los pesos y prevenir el sobreajuste.
2. Selección de Características: La selección de un subconjunto relevante de características puede mejorar significativamente el rendimiento del modelo. Métodos como la regularización L1 pueden ayudar a seleccionar características importantes al imponer una penalización que elimina características irrelevantes.
3. Normalización de Datos: La normalización de los datos de entrada puede ayudar a que la regularización sea más efectiva, asegurando que todas las características contribuyan de manera equilibrada al modelo.
Técnicas Específicas para el Manejo de Datos de Alta Dimensión
1. Regularización L1 (Lasso)
- Descripción: La regularización L1 añade una penalización basada en la suma de los valores absolutos de los pesos. Esta técnica tiende a forzar muchos pesos a cero, lo que resulta en un modelo más esparso y una forma de selección automática de características.
- Fórmula:
donde C es la función de costo original y λ es el parámetro de regularización.
- Descripción: La regularización L2 añade una penalización basada en la suma de los cuadrados de los pesos. Esta técnica tiende a distribuir la penalización de manera más uniforme y es útil para evitar que los pesos se vuelvan excesivamente grandes.
3. Regularización Elastic Net
- Descripción: Elastic Net combina las penalizaciones L1 y L2 para aprovechar los beneficios de ambas. Es especialmente útil cuando se enfrentan datos con alta multicolinealidad.
- Fórmula:
4. Dropout
- Descripción: Dropout es una técnica específica para redes neuronales que apaga aleatoriamente un porcentaje de neuronas durante el entrenamiento. Esto ayuda a evitar la dependencia excesiva en neuronas individuales y promueve la redundancia en la red.
- Implementación: Durante el entrenamiento, cada neurona tiene una probabilidad p de ser "apagada". Durante la inferencia, todas las neuronas están activas, pero sus salidas se escalan por el factor p.
5. Selección de Características Basada en Regularización
- Técnica: Utilizar la regularización para seleccionar características relevantes puede reducir la dimensionalidad del conjunto de datos. La regularización L1 es particularmente eficaz para esta tarea, ya que puede eliminar características irrelevantes al asignarles un peso cero.
6. Modelos Parciales y Ensambles
- Modelos Parciales: Entrenar múltiples modelos en diferentes subconjuntos de características y combinar sus predicciones puede mejorar la generalización y manejar la alta dimensionalidad de manera más efectiva.
- Ensambles: Técnicas de ensamble como bagging y boosting pueden ayudar a mejorar la robustez y el rendimiento de los modelos en datos de alta dimensión.
En resumen, La regularización es esencial para manejar los desafíos de los datos de alta dimensión en el análisis de datos y el aprendizaje automático. Mediante técnicas como la regularización L1, L2, Elastic Net y Dropout, es posible mejorar la capacidad de generalización de los modelos y prevenir el sobreajuste. Adaptar y considerar cuidadosamente la regularización en el contexto de datos de alta dimensión permite desarrollar modelos más robustos y eficaces, capaces de enfrentar la complejidad y la variabilidad inherentes a estos conjuntos de datos.
Campus
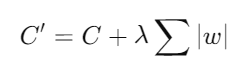2. Regularización L2 (Ridge)donde es la función de costo original y es el parámetro de regularización.- Descripción: La regularización L2 añade una penalización basada en la suma de los cuadrados de los pesos. Esta técnica tiende a distribuir la penalización de manera más uniforme y es útil para evitar que los pesos se vuelvan excesivamente grandes.
Campus
