Campus
Diagrama de temas
-
-
Introducción
El sobreajuste (overfitting) es un problema común en el análisis de datos y el aprendizaje automático, donde un modelo aprende demasiado bien los detalles y el ruido del conjunto de datos de entrenamiento. Este exceso de ajuste reduce la capacidad del modelo para generalizar y desempeñarse bien en nuevos datos no vistos. La regularización es una técnica esencial para mitigar el sobreajuste y mejorar la generalización de los modelos.
Contexto del Overfitting en el Análisis de Datos
El overfitting ocurre cuando un modelo se entrena demasiado en un conjunto de datos particular, capturando no solo los patrones subyacentes relevantes, sino también las peculiaridades y el ruido específicos de ese conjunto de datos. Este fenómeno es especialmente problemático en modelos complejos con alta capacidad, como las redes neuronales profundas, que tienen millones de parámetros y pueden aprender prácticamente cualquier relación en los datos de entrenamiento, incluso las que no son generalizables.
1. Causas del Overfitting:
- Modelo Complejo: Los modelos con demasiados parámetros tienden a ajustarse demasiado a los datos de entrenamiento.
- Datos Insuficientes: Un conjunto de datos de entrenamiento pequeño puede llevar a un modelo a aprender patrones específicos del conjunto en lugar de patrones generales.
- Ruido en los Datos: La presencia de ruido y outliers en los datos de entrenamiento puede desviar el aprendizaje del modelo hacia relaciones irrelevantes.
2. Consecuencias del Overfitting:
- Rendimiento Degradado en Nuevos Datos: Un modelo sobreajustado generalmente muestra un rendimiento excelente en el conjunto de datos de entrenamiento, pero un rendimiento pobre en datos de prueba o nuevos datos.
- Generalización Deficiente: La incapacidad del modelo para generalizar se traduce en predicciones inexactas y una falta de robustez ante variaciones en los datos de entrada.
Importancia de la Regularización
La regularización es una técnica crítica para prevenir el sobreajuste y mejorar la capacidad de generalización de los modelos de aprendizaje automático. La regularización introduce una penalización por la complejidad del modelo, limitando la capacidad del modelo para ajustarse demasiado a los datos de entrenamiento.
1. Técnicas de Regularización:- Regularización L2 (Ridge Regression): Esta técnica añade una penalización basada en la suma de los cuadrados de los pesos del modelo. Esto fuerza a los pesos a mantenerse pequeños, reduciendo la probabilidad de que el modelo se ajuste demasiado a los datos de entrenamiento.
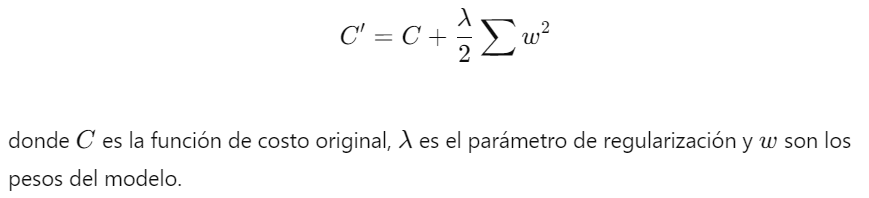
- Regularización L1 (Lasso Regression): Añade una penalización basada en la suma de los valores absolutos de los pesos. Esto puede llevar a la eliminación completa de algunos pesos, lo que resulta en un modelo más escaso.
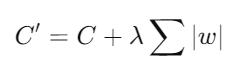
- Dropout: Una técnica específica para redes neuronales que apaga aleatoriamente un porcentaje de neuronas durante el entrenamiento, forzando a la red a no depender excesivamente de ninguna neurona en particular.
2. Beneficios de la Regularización:
- Mejora de la Generalización: Al penalizar la complejidad del modelo, la regularización ayuda a los modelos a aprender patrones generales en lugar de detalles específicos del conjunto de datos de entrenamiento.
- Reducción de la Varianza: La regularización puede ayudar a reducir la varianza del modelo, haciendo que sus predicciones sean más consistentes y menos sensibles a pequeñas variaciones en los datos de entrada.
- Evita el Overfitting: Al controlar la magnitud de los parámetros del modelo, la regularización minimiza el riesgo de que el modelo se ajuste demasiado a los datos de entrenamiento, mejorando así su rendimiento en datos no vistos.
En resumen, el sobreajuste es un desafío significativo en el análisis de datos y el aprendizaje automático, que puede degradar seriamente el rendimiento de un modelo en datos nuevos. La regularización es una técnica esencial para mitigar este problema, mejorando la capacidad de generalización de los modelos y asegurando predicciones más robustas y precisas. Al aplicar regularización, los investigadores y practicantes pueden desarrollar modelos más fiables y efectivos, capaces de enfrentar mejor las complejidades y variaciones de los datos del mundo real.
Enlace Adicional
Para más Información, acceda a este documento.
-
Fundamentos del Overfitting
El sobreajuste (overfitting) es uno de los principales desafíos en el campo del aprendizaje automático y el análisis de datos. Ocurre cuando un modelo se ajusta demasiado bien a los datos de entrenamiento, capturando no solo los patrones subyacentes, sino también el ruido y las peculiaridades del conjunto de datos específico. Esto puede llevar a un rendimiento deficiente en datos nuevos o no vistos. En este texto, exploraremos los fundamentos del overfitting, sus consecuencias en modelos de alta dimensión y proporcionaremos ejemplos prácticos para ilustrar este fenómeno.
Definición de Overfitting
El overfitting se define como el fenómeno en el cual un modelo de aprendizaje automático se ajusta excesivamente a los datos de entrenamiento, logrando un rendimiento muy alto en estos datos, pero fallando en generalizar a nuevos datos. En otras palabras, el modelo aprende tanto los patrones verdaderos como el ruido o las irregularidades específicas del conjunto de entrenamiento, lo que resulta en una capacidad de predicción pobre para datos no vistos.
1. Modelo Complejo: Los modelos con alta capacidad, como las redes neuronales profundas o los modelos con muchos parámetros, son particularmente susceptibles al overfitting. Estos modelos pueden aprender cualquier detalle del conjunto de datos de entrenamiento, incluyendo el ruido.
2. Falta de Datos: El sobreajuste es más probable cuando se dispone de un conjunto de datos de entrenamiento pequeño. En tales casos, el modelo puede aprender detalles específicos de estos datos en lugar de patrones generalizables.
3. Ruido en los Datos: La presencia de ruido y outliers en los datos de entrenamiento puede inducir al modelo a aprender relaciones irrelevantes.
Consecuencias del Overfitting en Modelos de Alta Dimensión
El overfitting puede tener consecuencias graves, especialmente en modelos de alta dimensión. Algunas de las principales consecuencias incluyen:
1. Rendimiento Degradado en Datos Nuevos: Un modelo sobreajustado suele mostrar un rendimiento excelente en el conjunto de datos de entrenamiento, pero un rendimiento deficiente en datos de prueba o nuevos datos. Esto se debe a que el modelo ha aprendido detalles específicos del conjunto de entrenamiento que no se aplican a datos no vistos.
2. Generalización Deficiente: La capacidad del modelo para generalizar se ve comprometida, lo que significa que no puede hacer predicciones precisas sobre datos no vistos. Esto es particularmente problemático en aplicaciones donde la precisión y la robustez son críticas.
3. Aumento de la Varianza: Los modelos sobreajustados tienden a tener alta varianza, lo que significa que son muy sensibles a pequeñas variaciones en los datos de entrada. Esto puede llevar a resultados inconsistentes y poco fiables.
Ejemplos Prácticos de Overfitting
Para ilustrar el fenómeno del overfitting, consideremos algunos ejemplos prácticos:
1. Clasificación de Imágenes: Supongamos que estamos entrenando una red neuronal profunda para clasificar imágenes de gatos y perros. Si la red es demasiado compleja y tenemos un conjunto de datos pequeño, la red puede aprender detalles específicos de las imágenes de entrenamiento, como el fondo de la imagen o la posición del animal, en lugar de características generales como la forma y textura del gato o el perro. Como resultado, la red puede clasificar correctamente las imágenes de entrenamiento pero fallar en nuevas imágenes de gatos y perros.
2. Predicción de Precios de Viviendas: En un modelo de regresión para predecir los precios de viviendas basado en características como el tamaño, la ubicación y el número de habitaciones, un modelo sobreajustado podría aprender relaciones espurias específicas del conjunto de datos de entrenamiento. Por ejemplo, podría aprender a asociar precios de viviendas con detalles irrelevantes como el color de la puerta o la fecha de construcción exacta, en lugar de factores verdaderamente importantes. Esto resultaría en predicciones inexactas para nuevas viviendas.
3. Modelos de Lenguaje Natural: En el procesamiento del lenguaje natural (NLP), un modelo de lenguaje como GPT puede sobreajustarse al corpus de entrenamiento si es demasiado complejo o si el corpus es pequeño. Esto puede hacer que el modelo genere texto que imita demasiado de cerca los ejemplos de entrenamiento, en lugar de producir respuestas originales y generalizables.
En resumen, el sobreajuste es un desafío crítico en el aprendizaje automático y el análisis de datos que puede comprometer la capacidad de un modelo para generalizar y hacer predicciones precisas en nuevos datos. Comprender las causas y las consecuencias del overfitting, así como reconocer ejemplos prácticos, es esencial para desarrollar modelos robustos y fiables. Las técnicas de regularización y la recolección de conjuntos de datos más grandes y diversos son estrategias clave para mitigar el sobreajuste y mejorar la generalización de los modelos.
Enlace Adicional
Para más Información, acceda a este documento.
-
Conceptos Básicos de Regularización
La regularización es una técnica fundamental en el aprendizaje automático utilizada para prevenir el sobreajuste (overfitting) y mejorar la capacidad de generalización de los modelos. El sobreajuste ocurre cuando un modelo se ajusta demasiado bien a los datos de entrenamiento, capturando tanto los patrones subyacentes como el ruido y las peculiaridades de esos datos, lo que resulta en un rendimiento deficiente en datos nuevos. En este texto, exploraremos la definición y el objetivo de la regularización, su relación con la capacidad del modelo y el trade-off entre sesgo y varianza.
1. Definición y Objetivo de la Regularización
- Definición: La regularización es un conjunto de técnicas utilizadas para añadir una penalización por complejidad al modelo durante el proceso de entrenamiento. Esta penalización se incluye en la función de costo que el modelo intenta minimizar, y su objetivo es restringir el ajuste excesivo del modelo a los datos de entrenamiento.
- Objetivo: El principal objetivo de la regularización es mejorar la capacidad de generalización del modelo. Esto se logra al evitar que el modelo aprenda patrones irrelevantes o ruidosos presentes en los datos de entrenamiento, permitiéndole así desempeñarse mejor en datos no vistos. En términos simples, la regularización ayuda a equilibrar la precisión del modelo en el conjunto de entrenamiento y su capacidad para generalizar a nuevos datos.
Relación entre Regularización y Capacidad del Modelo
La capacidad de un modelo se refiere a su habilidad para capturar patrones y relaciones complejas en los datos. Los modelos con alta capacidad, como las redes neuronales profundas, tienen muchos parámetros y pueden aprender prácticamente cualquier relación en los datos de entrenamiento. Sin embargo, esta alta capacidad también los hace propensos al sobreajuste.
Capacidad del Modelo:- Alta Capacidad: Un modelo con muchos parámetros puede ajustarse muy bien a los datos de entrenamiento, pero corre el riesgo de capturar ruido y peculiaridades específicas de esos datos.
- Baja Capacidad: Un modelo con pocos parámetros puede no ser capaz de capturar todas las relaciones complejas en los datos, resultando en un subajuste (underfitting).
La regularización actúa como un control sobre la capacidad del modelo, penalizando la complejidad excesiva y alentando a los modelos a ser más simples y robustos.
Trade-off entre Sesgo y Varianza
El trade-off entre sesgo y varianza es un concepto central en el aprendizaje automático que describe el equilibrio que debe alcanzarse para minimizar el error de predicción.
Sesgo:
El sesgo se refiere al error introducido por asumir que el modelo es demasiado simple para capturar la complejidad subyacente en los datos.
Un modelo con alto sesgo tiene una capacidad insuficiente y generalmente sufre de subajuste (underfitting).
Varianza:
- La varianza se refiere a la sensibilidad del modelo a pequeñas variaciones en los datos de entrenamiento.
- Un modelo con alta varianza tiene una capacidad excesiva y generalmente sufre de sobreajuste (overfitting).
Trade-off entre Sesgo y Varianza:
- La regularización ayuda a encontrar un equilibrio adecuado entre sesgo y varianza. Al añadir una penalización por complejidad, la regularización reduce la varianza del modelo al evitar que se ajuste demasiado a los datos de entrenamiento, mientras que un ajuste adecuado de la penalización ayuda a mantener el sesgo bajo control.
Un modelo bien regularizado tiene un equilibrio óptimo entre sesgo y varianza, lo que resulta en un rendimiento general robusto y una mejor capacidad de generalización.
En resumen, la regularización es una técnica esencial para mejorar la capacidad de generalización de los modelos de aprendizaje automático, controlando la capacidad del modelo y gestionando el trade-off entre sesgo y varianza. Al aplicar regularización, los modelos pueden evitar el sobreajuste, aprender patrones más generales y desempeñarse mejor en datos no vistos.
Enlace Adicional
Para más Información, acceda a este documento.
-
Técnicas Clásicas de Regularización
En el aprendizaje automático y la regresión estadística, la regularización es una técnica crucial para prevenir el sobreajuste y mejorar la capacidad de generalización de los modelos. Las técnicas clásicas de regularización, como Ridge Regression (L2), Lasso Regression (L1) y Elastic Net, son ampliamente utilizadas para controlar la complejidad de los modelos y asegurar un rendimiento robusto en datos no vistos. Este texto explora en detalle estos métodos, sus conceptos, fórmulas, aplicaciones y ventajas.
1. Ridge Regression (L2 Regularization)
Concepto y Fórmula
Ridge Regression, también conocida como regularización L2, es una técnica que añade una penalización a la función de costo basada en la suma de los cuadrados de los coeficientes del modelo. La fórmula de la función de costo regularizada es:
Aplicaciones y Ventajas
- Aplicaciones: Ridge Regression se utiliza principalmente en contextos donde los datos presentan multicolinealidad, es decir, cuando las variables independientes están altamente correlacionadas. Es útil en modelos de regresión lineal donde se busca estabilizar y mejorar las predicciones.- Ventajas:- Reducción del Overfitting: Al penalizar los coeficientes grandes, Ridge Regression reduce la varianza del modelo, ayudando a prevenir el sobreajuste.- Estabilidad: Proporciona soluciones estables incluso en presencia de multicolinealidad.- Simplicidad de Implementación: Es fácil de implementar y entender, lo que la hace una elección popular en muchas aplicaciones de regresión.2. Lasso Regression (L1 Regularization)
Concepto y Fórmula
Lasso Regression, o regularización L1, introduce una penalización basada en la suma de los valores absolutos de los coeficientes del modelo. La fórmula de la función de costo regularizada es:
Comparación con Ridge Regression
- Sparsity: Una de las características más destacadas de Lasso es su capacidad para producir modelos esparsos, es decir, modelos con muchos coeficientes exactamente iguales a cero. Esto facilita la selección de características y simplifica el modelo.
- Ventajas sobre Ridge:
- Selección de Características: Lasso puede eliminar completamente algunas características, lo que no ocurre con Ridge.
- Interpretabilidad: Los modelos resultantes de Lasso son más interpretables debido a la reducción de características innecesarias.
3. Elastic Net
Combinación de L1 y L2
Elastic Net es una técnica de regularización que combina las penalizaciones de L1 y L2, integrando las ventajas de ambos métodos. La fórmula de la función de costo regularizada es:
Ventajas y Casos de Uso
- Ventajas:
- Equilibrio entre Lasso y Ridge: Elastic Net combina la capacidad de selección de características de Lasso con la estabilidad de Ridge.
- Eficiencia en Altas Dimensiones: Es especialmente útil en problemas con un gran número de características, donde algunas de ellas están correlacionadas.
- Flexibilidad: Permite ajustar los parámetros para encontrar un equilibrio óptimo entre la selección de características y la estabilidad del modelo.
Casos de Uso:
Genómica y Biología Computacional: En estudios genéticos donde hay muchas variables correlacionadas.
Problemas de Altas Dimensiones: En cualquier problema de aprendizaje automático con muchas características y datos limitados.
En resumen, las técnicas clásicas de regularización, como Ridge Regression, Lasso Regression y Elastic Net, son herramientas esenciales para mejorar la generalización de los modelos y prevenir el sobreajuste. Cada técnica tiene sus propias ventajas y aplicaciones específicas, y la elección entre ellas depende del problema y los datos en cuestión. La comprensión y el uso adecuado de estas técnicas permiten desarrollar modelos más robustos y eficientes en una amplia gama de aplicaciones de aprendizaje automático y análisis de datos.
Enlace Adicional
Para más Información, acceda a este documento.
-
Regularización en Modelos No Lineales
La regularización es una técnica fundamental en el aprendizaje automático que se utiliza para prevenir el sobreajuste y mejorar la capacidad de generalización de los modelos. En los modelos no lineales, como las redes neuronales y las máquinas de soporte vectorial (SVM), la regularización desempeña un papel crucial en el control de la complejidad del modelo y en la mejora de su rendimiento en datos no vistos. En este texto, exploraremos diversas técnicas de regularización en deep learning, como el Dropout y el Early Stopping, así como la regularización en el espacio de características para las SVM.
Regularización en Redes Neuronales
Las redes neuronales son modelos altamente flexibles y potentes, pero también susceptibles al sobreajuste debido a su capacidad para modelar relaciones complejas en los datos. A continuación, se describen algunas técnicas de regularización comúnmente utilizadas en deep learning.
Técnicas de Regularización en Deep Learning
1. Regularización L2 (Decaimiento de Peso): Añade una penalización basada en la suma de los cuadrados de los pesos del modelo a la función de costo. Esto ayuda a mantener los pesos pequeños y evita que el modelo se ajuste demasiado a los datos de entrenamiento.
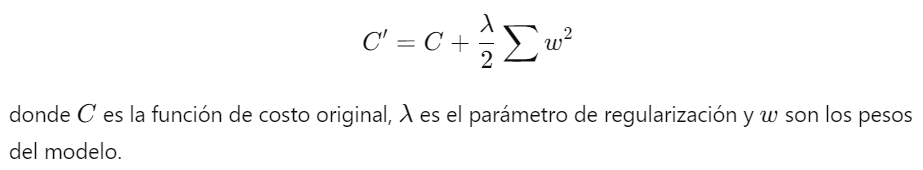
2. Regularización L1: Añade una penalización basada en la suma de los valores absolutos de los pesos. Esto puede llevar a la eliminación completa de algunos pesos, resultando en un modelo más esparso.
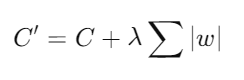
3. Dropout: Dropout es una técnica popular en la regularización de redes neuronales profundas.
Dropout: Definición y Funcionamiento
Dropout es una técnica de regularización que se utiliza para reducir el sobreajuste en redes neuronales al introducir ruido en la red durante el entrenamiento. El concepto principal de Dropout es desactivar (o "apagar") aleatoriamente un porcentaje de las neuronas en cada capa durante cada iteración de entrenamiento. Esto obliga a la red a aprender representaciones más robustas y a no depender excesivamente de ninguna neurona en particular.- Definición: Dropout consiste en eliminar aleatoriamente un porcentaje de las neuronas de la red en cada paso de entrenamiento. Durante la fase de prueba, todas las neuronas están activas, pero sus salidas se escalonan por el factor de Dropout (por ejemplo, si el 50% de las neuronas se eliminan durante el entrenamiento, las salidas se escalan por 0.5 durante la prueba).
- Funcionamiento: En cada iteración de entrenamiento, se selecciona aleatoriamente un subconjunto de neuronas para desactivarlas. Las conexiones de estas neuronas no se utilizan en ese paso, y sus contribuciones a la activación y la retropropagación se omiten.
Early Stopping: Concepto y Aplicación
Early Stopping es otra técnica de regularización que detiene el entrenamiento de la red neuronal antes de que el modelo comience a sobreajustarse a los datos de entrenamiento. La idea es monitorear el rendimiento del modelo en un conjunto de validación durante el entrenamiento y detener el proceso cuando el rendimiento en el conjunto de validación deja de mejorar.
- Concepto: Early Stopping se basa en la observación del error de validación durante el entrenamiento. Cuando el error de validación comienza a aumentar mientras el error de entrenamiento sigue disminuyendo, indica que el modelo está comenzando a sobreajustarse.
- Aplicación: Se divide el conjunto de datos en un conjunto de entrenamiento y un conjunto de validación. Durante el entrenamiento, se monitorea el rendimiento del modelo en el conjunto de validación. Si el rendimiento no mejora después de un número determinado de iteraciones (patience), el entrenamiento se detiene.
Regularización en Máquinas de Soporte Vectorial (SVM)
Las Máquinas de Soporte Vectorial (SVM) son modelos poderosos para la clasificación y la regresión, especialmente efectivos en espacios de alta dimensión. La regularización es crucial en SVM para controlar la complejidad del modelo y mejorar su generalización.
Introducción a las SVM
Las SVM son modelos supervisados que buscan encontrar el hiperplano que mejor separa las clases en un espacio de características. El objetivo es maximizar el margen entre las muestras de las diferentes clases, lo que se traduce en un modelo más robusto y generalizable.
Regularización en el Espacio de Características
1. Regularización en SVM Lineales: En las SVM lineales, la regularización se incorpora en el término de margen suave, que permite que algunas muestras estén dentro del margen o en el lado incorrecto del hiperplano. La función de costo se define como:
2. Regularización en SVM no Lineales: En las SVM no lineales, el kernel trick se utiliza para mapear los datos a un espacio de características de mayor dimensión donde se puede aplicar la regularización de manera similar a las SVM lineales. La elección del kernel y su parámetro también actúan como formas de regularización.
En resumen, la regularización es una técnica esencial en el aprendizaje automático, especialmente en modelos no lineales como las redes neuronales y las SVM. Técnicas como Dropout y Early Stopping en deep learning y la regularización en el espacio de características en SVM ayudan a prevenir el sobreajuste y mejorar la capacidad de generalización de los modelos. Estas técnicas permiten a los modelos aprender representaciones más robustas y efectivas, mejorando su rendimiento en datos no vistos y asegurando su aplicabilidad en el mundo real.Enlace Adicional
Para más Información, acceda a este documento.
-
Métodos de Regularización Basados en la Complejidad del Modelo
La regularización es una técnica esencial en el aprendizaje automático que ayuda a prevenir el sobreajuste (overfitting) y mejora la capacidad de generalización de los modelos. Entre los métodos de regularización más importantes se encuentran aquellos basados en la complejidad del modelo, los cuales penalizan modelos complejos para fomentar soluciones más simples y generalizables. En este texto, exploraremos dos enfoques principales: la penalización de normas y la regularización basada en la complejidad de la estructura, así como su aplicación en modelos jerárquicos y árboles de decisión.
Penalización de Normas
La penalización de normas es una técnica de regularización que introduce un término de penalización en la función de costo del modelo, basado en las normas de los parámetros del modelo. Las normas L1 y L2 son las más comunes, y también se pueden combinar para obtener beneficios adicionales.
Regularización Basada en la Norma del Modelo
1. Norma L1 (Lasso):
- Descripción: La regularización L1 añade una penalización proporcional a la suma de los valores absolutos de los pesos del modelo. Esto puede llevar a que algunos pesos se reduzcan a cero, promoviendo la esparsidad en el modelo.
- Fórmula:
C′ = C+λ∑∣w∣
donde es la función de costo original, es el parámetro de regularización y son los pesos del modelo.
- Ventajas: La esparsidad resultante puede ser útil para la selección de características y para interpretar el modelo, ya que elimina características irrelevantes.
2. Norma L2 (Ridge):
- Descripción: La regularización L2 añade una penalización proporcional a la suma de los cuadrados de los pesos del modelo, lo que fuerza a los pesos a mantenerse pequeños.
- Fórmula:
C ′ = C + λ 2 ∑ w 2 Ventajas: Ayuda a prevenir el sobreajuste al controlar la magnitud de los pesos, manteniendo todos los parámetros pero con valores más pequeños y estables.
3. Combinación de Normas L1 y L2 (Elastic Net):
- Descripción: La regularización Elastic Net combina las penalizaciones L1 y L2 para aprovechar los beneficios de ambas técnicas.
- Fórmula:
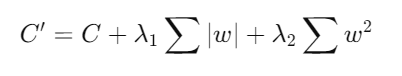
donde y son los parámetros de regularización para las normas L1 y L2, respectivamente.
Ventajas: Combina la esparsidad de Lasso con la estabilidad de Ridge, resultando en modelos más robustos y generalizables.
Regularización Basada en la Complejidad de la Estructura
La regularización basada en la complejidad de la estructura se enfoca en la forma y la complejidad interna del modelo. Este enfoque es particularmente útil en modelos jerárquicos y árboles de decisión.
Aplicación en Modelos Jerárquicos
- Modelos Jerárquicos:
- Descripción: Los modelos jerárquicos capturan relaciones entre variables en diferentes niveles de abstracción. La regularización en estos modelos puede involucrar la penalización de la complejidad de las dependencias entre niveles.
- Técnicas: Métodos como la regularización bayesiana y la selección de modelos jerárquicos pueden ayudar a simplificar la estructura del modelo y mejorar su capacidad de generalización.
Aplicación en Árboles de Decisión
Árboles de Decisión:
- Descripción: Los árboles de decisión son modelos de aprendizaje automático que segmentan los datos en subconjuntos basados en reglas de decisión. Sin regularización, los árboles de decisión tienden a sobreajustarse a los datos de entrenamiento.
- Técnicas de Regularización:
- Poda de Árboles: La poda de árboles reduce la complejidad del árbol eliminando ramas que tienen un impacto mínimo en la precisión de la predicción.
- Penalización de la Profundidad: Limitar la profundidad máxima del árbol ayuda a prevenir el sobreajuste, forzando al modelo a tomar decisiones basadas en características más generales.
Importancia de la RegularizaciónLa regularización es fundamental para desarrollar modelos que no solo se ajusten bien a los datos de entrenamiento, sino que también generalicen bien a datos no vistos. Al introducir penalizaciones basadas en la complejidad del modelo, se promueve la simplicidad y se evita que el modelo se ajuste a las particularidades y el ruido del conjunto de datos de entrenamiento. Esto resulta en modelos más robustos y precisos en diversas aplicaciones del mundo real.
Enlace Adicional
Para más información, acceda a este sitio.
-
Regularización en el Contexto de Datos de Alta Dimensión
En el análisis de datos y el aprendizaje automático, los datos de alta dimensión presentan desafíos únicos que pueden complicar el proceso de modelado y aumentar el riesgo de sobreajuste (overfitting). La regularización se vuelve especialmente crucial en este contexto para mejorar la capacidad de generalización de los modelos. En este texto, exploraremos los desafíos específicos de los datos de alta dimensión, las adaptaciones y consideraciones para la regularización, y las técnicas específicas para manejar estos datos.
Desafíos Específicos de los Datos de Alta Dimensión
1. Mal de la Dimensionalidad: A medida que aumenta el número de dimensiones (características), el espacio de características se vuelve exponencialmente grande, haciendo que los datos se dispersen. Esto dificulta la detección de patrones significativos y puede conducir a un rendimiento deficiente del modelo.2. Sobreajuste: Con muchos más parámetros que ejemplos, los modelos pueden aprender ruido en lugar de patrones subyacentes, lo que resulta en un alto riesgo de sobreajuste. Los modelos complejos tienden a ajustarse demasiado a los datos de entrenamiento, capturando detalles específicos y fallando en generalizar.3. Cálculo y Almacenamiento: Los datos de alta dimensión requieren mayor capacidad de almacenamiento y potencia computacional, lo que puede hacer que el entrenamiento y la implementación del modelo sean más costosos y lentos.Adaptaciones y Consideraciones para la Regularización
1. Penalización de la Magnitud de los Pesos: En datos de alta dimensión, es crucial limitar la magnitud de los pesos para evitar modelos demasiado complejos. Las técnicas como la regularización L1 y L2 ayudan a controlar los pesos y prevenir el sobreajuste.
2. Selección de Características: La selección de un subconjunto relevante de características puede mejorar significativamente el rendimiento del modelo. Métodos como la regularización L1 pueden ayudar a seleccionar características importantes al imponer una penalización que elimina características irrelevantes.
3. Normalización de Datos: La normalización de los datos de entrada puede ayudar a que la regularización sea más efectiva, asegurando que todas las características contribuyan de manera equilibrada al modelo.Técnicas Específicas para el Manejo de Datos de Alta Dimensión
1. Regularización L1 (Lasso)- Descripción: La regularización L1 añade una penalización basada en la suma de los valores absolutos de los pesos. Esta técnica tiende a forzar muchos pesos a cero, lo que resulta en un modelo más esparso y una forma de selección automática de características.- Fórmula: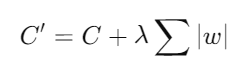
2. Regularización L2 (Ridge)donde es la función de costo original y es el parámetro de regularización.- Descripción: La regularización L2 añade una penalización basada en la suma de los cuadrados de los pesos. Esta técnica tiende a distribuir la penalización de manera más uniforme y es útil para evitar que los pesos se vuelvan excesivamente grandes.- Fórmula:
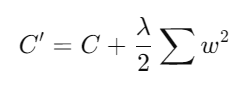
3. Regularización Elastic Net
- Descripción: Elastic Net combina las penalizaciones L1 y L2 para aprovechar los beneficios de ambas. Es especialmente útil cuando se enfrentan datos con alta multicolinealidad.
- Fórmula:
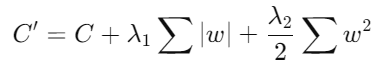
4. Dropout
- Descripción: Dropout es una técnica específica para redes neuronales que apaga aleatoriamente un porcentaje de neuronas durante el entrenamiento. Esto ayuda a evitar la dependencia excesiva en neuronas individuales y promueve la redundancia en la red.
- Implementación: Durante el entrenamiento, cada neurona tiene una probabilidad p de ser "apagada". Durante la inferencia, todas las neuronas están activas, pero sus salidas se escalan por el factor p.
5. Selección de Características Basada en Regularización
- Técnica: Utilizar la regularización para seleccionar características relevantes puede reducir la dimensionalidad del conjunto de datos. La regularización L1 es particularmente eficaz para esta tarea, ya que puede eliminar características irrelevantes al asignarles un peso cero.
6. Modelos Parciales y Ensambles
- Modelos Parciales: Entrenar múltiples modelos en diferentes subconjuntos de características y combinar sus predicciones puede mejorar la generalización y manejar la alta dimensionalidad de manera más efectiva.
- Ensambles: Técnicas de ensamble como bagging y boosting pueden ayudar a mejorar la robustez y el rendimiento de los modelos en datos de alta dimensión.
En resumen, La regularización es esencial para manejar los desafíos de los datos de alta dimensión en el análisis de datos y el aprendizaje automático. Mediante técnicas como la regularización L1, L2, Elastic Net y Dropout, es posible mejorar la capacidad de generalización de los modelos y prevenir el sobreajuste. Adaptar y considerar cuidadosamente la regularización en el contexto de datos de alta dimensión permite desarrollar modelos más robustos y eficaces, capaces de enfrentar la complejidad y la variabilidad inherentes a estos conjuntos de datos.
-
Regularización y Selección de Variables
En el contexto del aprendizaje automático y la estadística, la regularización y la selección de variables son técnicas fundamentales para manejar modelos de alta dimensión. En modelos con un gran número de variables, es crucial seleccionar las más relevantes para mejorar la interpretabilidad y el rendimiento del modelo. La regularización ayuda a prevenir el sobreajuste y facilita la selección de variables de manera integrada. Este texto explorará la importancia de la selección de variables, los métodos de selección de variables integrados con regularización y las técnicas de reducción de dimensionalidad como regularización implícita.
Importancia de la Selección de Variables en Modelos de Alta Dimensión
En modelos con un gran número de variables, es común que muchas de ellas sean irrelevantes o redundantes. Incluir estas variables innecesarias puede llevar a problemas como el sobreajuste, donde el modelo aprende el ruido en los datos en lugar de los patrones subyacentes. La selección de variables es crucial por varias razones:
1. Mejora de la Interpretabilidad: Reducir el número de variables facilita la comprensión del modelo y su interpretación, lo que es especialmente importante en aplicaciones donde la explicabilidad es crucial.
2. Reducción de la Varianza: Eliminar variables irrelevantes puede reducir la varianza del modelo, mejorando su capacidad de generalización a nuevos datos.
3. Eficiencia Computacional: Trabajar con un menor número de variables reduce los requisitos computacionales, lo que es beneficioso para el entrenamiento y la implementación del modelo.
Métodos de Selección de Variables Integrados con Regularización
Los métodos de selección de variables integrados con regularización combinan la penalización de la complejidad del modelo con la eliminación de variables irrelevantes. Algunos de los métodos más comunes incluyen:
1. Lasso (Least Absolute Shrinkage and Selection Operator)
- Descripción: Lasso añade una penalización L1 a la función de costo del modelo, lo que fuerza a que algunos coeficientes se reduzcan exactamente a cero, eliminando así variables irrelevantes.
- Fórmula:
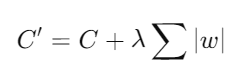
donde C es la función de costo original, λ es el parámetro de regularización, y w son los coeficientes del modelo.
- Ventajas: Lasso realiza automáticamente la selección de variables y puede manejar grandes conjuntos de datos de manera eficiente.
2. Elastic Net
- Descripción: Elastic Net combina las penalizaciones L1 y L2, proporcionando un balance entre la selección de variables de Lasso y la regularización de Ridge.
- Fórmula:
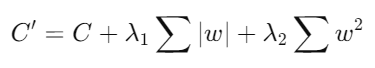
- Ventajas: Elastic Net es útil cuando hay correlación entre variables, ya que puede seleccionar grupos de variables correlacionadas en lugar de eliminar una sola variable de cada grupo.
Técnicas de Reducción de Dimensionalidad como Regularización ImplícitaLas técnicas de reducción de dimensionalidad también actúan como una forma de regularización implícita al transformar los datos en un espacio de menor dimensión, manteniendo las características más importantes. Algunas de estas técnicas incluyen:
1. Análisis de Componentes Principales (PCA)
- Descripción: PCA transforma los datos originales en un nuevo conjunto de variables no correlacionadas llamadas componentes principales. Estas componentes son combinaciones lineales de las variables originales y están ordenadas por la cantidad de varianza que explican en los datos.
- Ventajas: PCA reduce la dimensionalidad de los datos y puede mejorar el rendimiento del modelo al eliminar el ruido y las redundancias.
2. Análisis de Componentes Independientes (ICA)
- Descripción: ICA busca encontrar componentes independientes en los datos que maximicen la independencia estadística. Es útil en aplicaciones donde las fuentes de los datos son independientes.
- Ventajas: ICA es particularmente útil para el análisis de señales y puede descomponer datos complejos en componentes más interpretables.
En resumen, la selección de variables y la regularización son técnicas cruciales en el manejo de modelos de alta dimensión. La integración de métodos de regularización como Lasso y Elastic Net permite la selección automática de variables, mejorando la interpretabilidad y el rendimiento del modelo. Además, las técnicas de reducción de dimensionalidad como PCA e ICA actúan como formas de regularización implícita, ayudando a reducir la complejidad del modelo y mejorar su capacidad de generalización. Estas estrategias son esenciales para desarrollar modelos robustos y eficientes en el análisis de datos y el aprendizaje automático.
-
Técnicas Avanzadas de Regularización
La regularización es una técnica fundamental en el aprendizaje automático para prevenir el sobreajuste y mejorar la generalización de los modelos. Más allá de las técnicas clásicas como L1 y L2, existen métodos avanzados de regularización que se adaptan a problemas más específicos y complejos. En este texto, exploraremos tres técnicas avanzadas de regularización: Regularización de Grupo (Group Lasso), Regularización de Matrices (Matrix Regularization) y Regularización Bayesiana, explicando sus aplicaciones y ventajas.
Regularización de Grupo (Group Lasso)
Aplicación a la Selección de Grupos de Variables
Group Lasso es una extensión de la regularización Lasso que se utiliza para la selección de grupos de variables en lugar de variables individuales. Este método es especialmente útil cuando las variables están naturalmente agrupadas, y se desea seleccionar o eliminar grupos completos en lugar de variables individuales.
1. Descripción del Método: En Group Lasso, las variables se agrupan en conjuntos, y se aplica una penalización a la suma de las normas L2 de los coeficientes dentro de cada grupo. La función de costo para Group Lasso se define como:
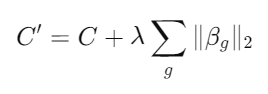donde es el vector de coeficientes del grupo y es el parámetro de regularización.2. Ventajas:
- Selección de Grupos: Permite seleccionar grupos completos de variables, lo cual es beneficioso cuando las variables dentro de un grupo están altamente correlacionadas.
- Interpretabilidad: Facilita la interpretabilidad del modelo al mantener o eliminar grupos completos de características.
3. Aplicaciones: Group Lasso es útil en aplicaciones donde las variables están organizadas en grupos, como en el análisis de imágenes, genómica y señales de tiempo.
Regularización de Matrices (Matrix Regularization)
Aplicación en Problemas de Recomendación y Factorización de Matrices
La regularización de matrices se utiliza en problemas donde los datos pueden representarse en forma de matrices, como en sistemas de recomendación y factorización de matrices.1. Descripción del Método: En problemas de recomendación, se busca factorizar una matriz de interacciones (por ejemplo, usuarios y productos) en dos matrices de menor rango. La regularización se aplica para evitar el sobreajuste y mejorar la generalización de la factorización.
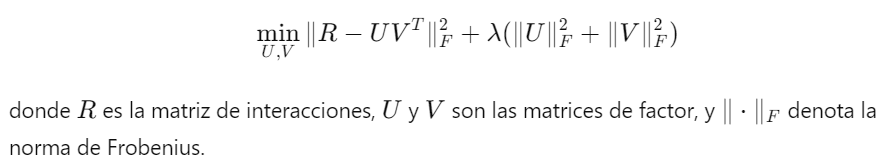
2. Ventajas:
- Reducción de la Complejidad: La regularización ayuda a evitar que las matrices factorizadas capturen demasiado ruido en los datos.
- Mejora de la Generalización: Al controlar la magnitud de los valores en las matrices factorizadas, se mejora la capacidad del modelo para generalizar a nuevos datos.
3. Aplicaciones: La regularización de matrices es ampliamente utilizada en sistemas de recomendación, como la recomendación de productos en plataformas de comercio electrónico y servicios de streaming.
Regularización Bayesiana
Enfoques Bayesianos para la Regularización
La regularización bayesiana introduce una perspectiva probabilística al problema de la regularización, incorporando conocimientos previos en la modelización.
1. Descripción del Método: En la regularización bayesiana, los parámetros del modelo se tratan como variables aleatorias y se definen distribuciones previas sobre ellos. La inferencia se realiza mediante la combinación de la información de los datos (verosimilitud) con la información previa (prior), resultando en la distribución posterior.
2. Comparación con Métodos Frecuentistas:
- Flexibilidad: Los métodos bayesianos permiten la incorporación explícita de conocimientos previos, lo que puede ser ventajoso en situaciones con datos limitados.
- Inferencia Completa: Proporcionan una distribución completa sobre los parámetros, permitiendo una evaluación más rica de la incertidumbre.
- Computacionalmente Intensivo: Los enfoques bayesianos pueden ser más complejos y requerir técnicas de muestreo como MCMC (Markov Chain Monte Carlo) para la inferencia.
En resumen, las técnicas avanzadas de regularización, como Group Lasso, la regularización de matrices y la regularización bayesiana, ofrecen poderosas herramientas para mejorar la generalización de los modelos de aprendizaje automático y prevenir el sobreajuste. Cada técnica se adapta a diferentes contextos y problemas específicos, proporcionando flexibilidad y robustez en la construcción de modelos predictivos precisos y confiables.3. Aplicaciones: La regularización bayesiana es utilizada en diversas áreas, incluyendo la estimación de modelos con datos escasos, la detección de anomalías y la modelización predictiva con altos niveles de incertidumbre.
Enlace Adicional
Para más información, visite este sitio.
-
Implementaciones y Casos de Estudio
La regularización es una técnica fundamental en el aprendizaje automático que se utiliza para mejorar la generalización de los modelos y prevenir el sobreajuste. Este documento se basa en el material del artículo académico "arxiv.org/pdf/1710.10686" y aborda implementaciones y casos de estudio que ilustran aplicaciones prácticas de diversas técnicas de regularización, comparaciones de efectividad en diferentes contextos y resultados empíricos junto con lecciones aprendidas.
Implementaciones y Casos de Estudio
Aplicaciones Prácticas de Técnicas de Regularización
Las técnicas de regularización son ampliamente utilizadas en diversas aplicaciones de aprendizaje automático para mejorar el rendimiento y la robustez de los modelos. A continuación se presentan algunas aplicaciones prácticas:1. Regularización L2 (Ridge Regression):
- Visión por Computadora: En tareas de clasificación de imágenes, la regularización L2 se aplica para reducir la complejidad del modelo, lo que ayuda a prevenir el sobreajuste y mejorar la precisión en datos de prueba.- Reconocimiento de Voz: En modelos de reconocimiento de voz, la regularización L2 ayuda a controlar la magnitud de los parámetros del modelo, resultando en una mejor generalización a diferentes acentos yentonaciones.2. Dropout:- Redes Neuronales Profundas: Dropout se utiliza comúnmente en redes neuronales profundas para prevenir el sobreajuste al apagar aleatoriamente un porcentaje de neuronas durante el entrenamiento. Esto ha demostrado ser efectivo en modelos como las redes convolucionales (CNN) y las redes recurrentes (RNN).
- Procesamiento del Lenguaje Natural (NLP): En tareas de procesamiento del lenguaje natural, Dropout ayuda a mejorar la robustez de los modelos en la generación de texto y la traducción automática.3. Regularización L1 (Lasso Regression):Selección de Características: En problemas de selección de características, la regularización L1 se utiliza para forzar a que algunos coeficientes sean exactamente cero, lo que resulta en modelos más simples y interpretables.Comparación de Efectividad en Diferentes Contextos
La efectividad de las técnicas de regularización puede variar según el contexto y la naturaleza del problema. A continuación se comparan algunas de estas técnicas en diferentes escenarios:
1. Visión por Computadora vs. Procesamiento del Lenguaje Natural:
- En visión por computadora, Dropout y la regularización L2 suelen ser más efectivos debido a la alta dimensionalidad y la complejidad de las características visuales.
- En procesamiento del lenguaje natural, técnicas como la regularización L1 y Dropout son cruciales para manejar la variabilidad en los datos de texto y mejorar la generalización a diferentes contextos lingüísticos.
2. Modelos Lineales vs. Modelos No Lineales:
- Para modelos lineales, la regularización L1 y L2 son métodos estándar que ayudan a prevenir el sobreajuste y mejorar la interpretabilidad del modelo.
- En modelos no lineales como las redes neuronales profundas, técnicas como Dropout y Batch Normalization son más adecuadas para controlar la complejidad del modelo y mejorar su capacidad de generalización.
Resultados Empíricos y Lecciones Aprendidas
Los estudios empíricos sobre la efectividad de las técnicas de regularización proporcionan información valiosa sobre su rendimiento en la práctica. A continuación se presentan algunos resultados clave y lecciones aprendidas:1. Regularización L2:
- Resultados: La regularización L2 ha demostrado ser efectiva para mejorar la precisión en tareas de clasificación y regresión, especialmente en modelos con muchas características.
- Lecciones Aprendidas: La elección del parámetro de regularización λ es crucial y generalmente se optimiza mediante validación cruzada para obtener el mejor rendimiento.
2. Dropout:
- Resultados: Dropout ha mostrado mejoras significativas en la precisión de modelos profundos en una variedad de tareas, desde la visión por computadora hasta el procesamiento del lenguaje natural.
- Lecciones Aprendidas: La tasa de Dropout óptima varía según la arquitectura del modelo y la tarea específica. Un ajuste cuidadoso es necesario para equilibrar la prevención del sobreajuste y la retención de suficiente capacidad de aprendizaje.
3. Regularización L1:
- Resultados: La regularización L1 es especialmente útil en la selección de características y ha demostrado mejorar la interpretabilidad de los modelos sin sacrificar significativamente la precisión.
- Lecciones Aprendidas: La regularización L1 puede llevar a modelos más esparsos, lo que facilita la interpretación, pero puede requerir ajustes finos para equilibrar entre esparsidad y rendimiento.
En resumen, la regularización es una herramienta indispensable en el aprendizaje automático, con aplicaciones prácticas que abarcan desde la visión por computadora hasta el procesamiento del lenguaje natural. Las técnicas de regularización como L2, Dropout y L1 han demostrado ser efectivas en diferentes contextos, y los resultados empíricos subrayan la importancia de ajustar adecuadamente los parámetros de regularización para maximizar el rendimiento del modelo. Las lecciones aprendidas de estos estudios empíricos son valiosas para guiar futuras aplicaciones y optimizaciones en la implementación de modelos de aprendizaje automático.
Enlace Adicional
Para más información, visite este sitio.
-
Conclusiones y Desafíos Futuros en Regularización
El uso de técnicas de regularización es crucial para mejorar la capacidad de generalización de los modelos de aprendizaje automático y prevenir el sobreajuste. A lo largo del tiempo, diversas técnicas han sido desarrolladas y probadas, mostrando efectividad en una amplia gama de aplicaciones. A continuación, se presenta un resumen de las técnicas discutidas, su efectividad, y los desafíos y áreas de investigación futuras en el campo de la regularización, así como las implicaciones para el diseño de modelos de aprendizaje automático.
Resumen de las Técnicas y su Efectividad
1. Regularización L2 (Ridge Regression):
- Efectividad: Esta técnica es efectiva para reducir la complejidad del modelo al penalizar grandes pesos, lo que ayuda a prevenir el sobreajuste. Es ampliamente utilizada debido a su simplicidad y su capacidad para mantener todos los pesos pequeños, promoviendo una solución más suave.
- Aplicación: Comúnmente utilizada en modelos lineales y redes neuronales, especialmente cuando se necesita un balance entre simplicidad y rendimiento.
2. Regularización L1 (Lasso Regression):
- Efectividad: La regularización L1 no solo penaliza grandes pesos, sino que también puede forzar a algunos pesos a ser exactamente cero, resultando en modelos esparsos. Esto puede ser útil para la selección de características y para interpretar mejor el modelo.
- Aplicación: Utilizada en situaciones donde la interpretabilidad y la esparsidad del modelo son importantes, como en problemas de selección de características.
3. Dropout:
- Efectividad: Dropout es particularmente efectivo en redes neuronales profundas. Al apagar aleatoriamente neuronas durante el entrenamiento, fuerza a la red a aprender representaciones redundantes, mejorando la robustez y la generalización.
- Aplicación: Ampliamente adoptado en modelos de redes neuronales para tareas de visión por computadora, procesamiento de lenguaje natural y más.
4. Regularización Basada en la Estructura:
- Efectividad: Estas técnicas consideran la estructura del modelo, penalizando no solo los pesos individuales sino también combinaciones y relaciones entre ellos. Esto puede ser particularmente útil en modelos jerárquicos y árboles de decisión.
- Aplicación: Utilizada en modelos más complejos donde las relaciones estructurales son importantes, como en redes neuronales convolucionales y modelos de árboles de decisión.
Desafíos y Áreas de Investigación Futuras en Regularización
1. Automatización de la Regularización:
- Desafío: Determinar automáticamente los parámetros óptimos de regularización (como el valor de lambda en L2) sigue siendo un desafío. La automatización de este proceso podría mejorar significativamente el diseño y la implementación de modelos.
- Investigación Futura: Desarrollo de algoritmos de aprendizaje que puedan ajustar dinámicamente los parámetros de regularización durante el entrenamiento.
2. Regularización en Modelos Complejos:
- Desafío: Aplicar técnicas de regularización efectivas a modelos complejos como redes neuronales profundas y redes generativas antagónicas (GAN) sin comprometer su capacidad de aprendizaje.
- Investigación Futura: Innovar en técnicas de regularización que sean específicas para arquitecturas avanzadas, incluyendo la integración de conocimientos del dominio y restricciones basadas en la estructura.
3. Interpretabilidad y Explicabilidad:
- Desafío: A medida que los modelos se vuelven más complejos, entender y explicar cómo las técnicas de regularización afectan el comportamiento del modelo se vuelve más difícil.
- Investigación Futura: Desarrollar métodos que no solo regularicen los modelos, sino que también mejoren su interpretabilidad y explicabilidad.
Implicaciones para el Diseño de Modelos de Aprendizaje Automático
1. Mejora de la Generalización: La incorporación de técnicas de regularización en el diseño de modelos es crucial para mejorar la capacidad de generalización, asegurando que los modelos funcionen bien en datos no vistos.
2. Simplicidad y Robustez: Los modelos regularizados tienden a ser más simples y robustos, lo que facilita su implementación y mantenimiento en aplicaciones del mundo real.
3. Equilibrio entre Complejidad y Rendimiento: Es esencial encontrar un equilibrio adecuado entre la complejidad del modelo y su rendimiento. La regularización ayuda a evitar modelos excesivamente complejos que no generalizan bien.
En resumen, la regularización es una técnica esencial en el aprendizaje automático que ayuda a mitigar el sobreajuste y mejorar la capacidad de generalización de los modelos. A medida que la investigación avanza, la exploración de nuevas técnicas y la mejora de las existentes continuarán siendo áreas críticas para el desarrollo de modelos más efectivos y robustos. La integración de técnicas de regularización en el diseño de modelos es fundamental para avanzar en la creación de soluciones de aprendizaje automático que sean eficientes, interpretables y capaces de enfrentar desafíos complejos en diversos dominios.
Enlace Adicional
Para más información, visite este sitio.
-
-
Campus
