 Campus
Campus
Diagrama de temas
-
Optimización en Redes Neuronales
La optimización es un proceso esencial en el entrenamiento de redes neuronales, cuyo objetivo es ajustar los parámetros del modelo (principalmente los pesos y biases) para minimizar la función de costo. Existen varios métodos de optimización que se utilizan para este propósito, cada uno con sus propias ventajas y desventajas. Además, el ajuste adecuado de los hiperparámetros es crucial para mejorar el rendimiento del modelo. En este texto, exploraremos algunos de los métodos de optimización más comunes y proporcionaremos una guía sobre cómo seleccionar y ajustar los hiperparámetros.
Métodos de Optimización
1. Gradiente Descendente Estocástico (SGD)- Descripción: El Gradiente Descendente Estocástico es una variante del gradiente descendente que actualiza los pesos del modelo utilizando un solo ejemplo de entrenamiento a la vez. Esto introduce ruido en el proceso de actualización, lo que puede ayudar a escapar de los mínimos locales.
- Fórmula de Actualización:
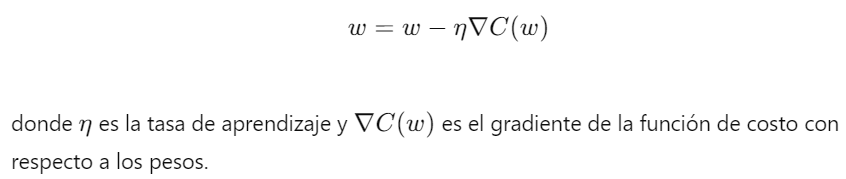
- Ventajas: SGD es simple y eficiente en términos de memoria, y puede converger más rápido que el gradiente descendente batch para grandes conjuntos de datos.
- Desventajas: La actualización ruidosa puede dificultar la convergencia y provocar oscilaciones alrededor del mínimo.
2. Adam (Adaptive Moment Estimation)
- Descripción: Adam es un método de optimización que combina las ventajas de dos técnicas: AdaGrad y RMSProp. Utiliza estimaciones adaptativas de momentos de primer y segundo orden.
- Fórmulas de Actualización:
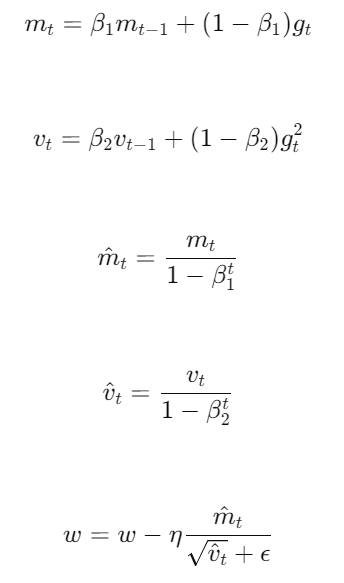
donde es el gradiente en el tiempo y son los estimados de primer y segundo momento, es la tasa de aprendizaje, y son parámetros de decaimiento exponencial, y es un término de estabilidad numérica.
- Ventajas: Adam es robusto y eficiente en términos de memoria, y generalmente funciona bien en una amplia variedad de problemas.
- Desventajas: Puede ser sensible a la configuración de hiperparámetros y, en algunos casos, puede no generalizar tan bien como SGD.3. Otros Métodos de Optimización
- RMSProp: Similar a AdaGrad, pero con un decaimiento exponencial de los gradientes pasados. Es útil para problemas donde la tasa de aprendizaje decreciente de AdaGrad es demasiado agresiva.
- AdaGrad: Ajusta la tasa de aprendizaje para cada parámetro, haciéndola más pequeña a medida que aumenta el número de actualizaciones. Es útil para características esparsas pero puede resultar en tasas de aprendizaje demasiado pequeñas.
- Momentum: Añade un término que acumula las actualizaciones pasadas, lo que ayuda a acelerar la convergencia en la dirección correcta y a reducir las oscilaciones.
Ajuste de Hiperparámetros
El ajuste de hiperparámetros es crucial para mejorar el rendimiento de una red neuronal. Aquí se presentan algunas estrategias para seleccionar y ajustar los hiperparámetros:
1. Tasa de Aprendizaje ():- Importancia: Controla la magnitud de las actualizaciones de los pesos. Una tasa de aprendizaje demasiado alta puede provocar divergencia, mientras que una demasiado baja puede hacer que el modelo tarde mucho en converger.- Ajuste: Comenzar con valores estándar (como 0.01) y ajustar gradualmente mediante validación cruzada.2. Tamaño del Batch:- Importancia: Afecta la estabilidad y la eficiencia del entrenamiento. Batches más grandes proporcionan estimaciones del gradiente más precisas, pero requieren más memoria.- Ajuste: Experimentar con diferentes tamaños de batch (como 32, 64, 128) y evaluar su impacto en la velocidad de convergencia y la precisión.3. Número de Épocas:- Importancia: Determina cuántas veces el modelo verá el conjunto de entrenamiento completo. Un número insuficiente de épocas puede resultar en un modelo infraajustado, mientras que demasiadas épocas pueden llevar al sobreajuste.- Ajuste: Utilizar la validación cruzada para detener el entrenamiento cuando el rendimiento en el conjunto de validación comience a empeorar.4. Parámetros Específicos de los Optimizadores:- Adam (): Valores típicos son y .
- Momentum: Un valor común es 0.9, pero puede ser ajustado según el problema.
Regularización (Dropout, L2):- Dropout Rate: Generalmente se establece entre 0.2 y 0.5.- Factor de Regularización L2 (): Un valor pequeño (como 0.0001) es un buen punto de partida, ajustándolo según el rendimiento de validación.Importancia del Ajuste de Hiperparámetros
El ajuste de hiperparámetros es crucial para maximizar el rendimiento del modelo y evitar problemas como el sobreajuste o el infraajuste. Un ajuste adecuado de los hiperparámetros puede mejorar significativamente la precisión y la capacidad de generalización del modelo, haciendo que sea más robusto y eficiente en una variedad de tareas y conjuntos de datos.
Enlace Adicional
Para más información acceda a este sitio.

