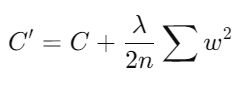Regularización en Redes Neuronales
La regularización es una técnica crucial en el entrenamiento de redes neuronales que ayuda a prevenir el sobreajuste (overfitting) y mejorar la capacidad de generalización del modelo. El sobreajuste ocurre cuando un modelo se ajusta demasiado a los datos de entrenamiento, capturando el ruido y las particularidades del conjunto de datos específico en lugar de aprender patrones generalizables. Para abordar este problema, se utilizan varios métodos de regularización que penalizan la complejidad del modelo. En este texto, exploraremos algunos de los métodos de regularización más comunes, como el Dropout y la regularización L2, y discutiremos la importancia de la regularización para mejorar la generalización del modelo.
Métodos de Regularización
1. Dropout
- Descripción: Dropout es una técnica de regularización en la que, durante el entrenamiento, se eliminan aleatoriamente (se ponen a cero) un porcentaje de las unidades (neuronas) de la red en cada iteración. Esto impide que las neuronas dependan demasiado unas de otras y fuerza a la red a aprender representaciones más robustas y generalizables.
- Implementación: En cada paso de entrenamiento, cada neurona tiene una probabilidad 𝑝 de ser "apagada". Durante la fase de prueba, todas las neuronas están activas, pero sus salidas se escalonan por el factor 𝑝 para mantener la consistencia en las magnitudes de las salidas.
- Ventajas: Dropout es efectivo en la reducción del sobreajuste y es fácil de implementar. Además, introduce un tipo de ensemblado de redes neuronales durante el entrenamiento, lo que mejora la robustez del modelo.
2. Regularización L2 (Penalización de Peso)
- Descripción: La regularización L2, también conocida como decaimiento de peso, añade una penalización al error de la función de costo basada en la magnitud de los pesos de la red. La idea es evitar que los pesos se vuelvan demasiado grandes, lo que puede llevar a un modelo más complejo y propenso al sobreajuste.
- Fórmula: La función de costo con regularización L2 se define como:
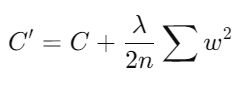
donde C es la función de costo original, λ es el parámetro de regularización que controla la fuerza de la penalización, n es el número de ejemplos de entrenamiento, y w son los pesos de la red.
- Ventajas: La regularización L2 ayuda a mantener los pesos pequeños, promoviendo un modelo más simple y menos propenso al sobreajuste. Es particularmente útil en modelos con muchas características o parámetros.
Importancia de la Regularización
La regularización juega un papel fundamental en la mejora de la generalización de los modelos de redes neuronales por varias razones:
1. Prevención del Sobreajuste: Al penalizar la complejidad del modelo y evitar que los pesos crezcan demasiado, la regularización ayuda a que el modelo no se ajuste demasiado a los datos de entrenamiento. Esto es esencial para que el modelo pueda generalizar bien a nuevos datos no vistos durante el entrenamiento.
2. Mejora de la Robustez del Modelo: Técnicas como Dropout introducen un grado de aleatoriedad durante el entrenamiento, lo que fuerza a la red a aprender representaciones más robustas y menos dependientes de combinaciones específicas de neuronas.
3. Reducción de la Varianza: La regularización puede ayudar a reducir la varianza del modelo, haciendo que sus predicciones sean más estables y menos sensibles a pequeñas variaciones en los datos de entrada.
4. Promoción de la Simplicidad del Modelo: Al imponer una penalización sobre la magnitud de los pesos, la regularización fomenta modelos más simples que tienden a ser más interpretables y a tener mejor rendimiento en datos no vistos.
En conclusión, la regularización es una técnica vital para el entrenamiento efectivo de redes neuronales, ya que ayuda a prevenir el sobreajuste y mejora la capacidad de generalización del modelo. Métodos como Dropout y la regularización L2 son herramientas poderosas que permiten a los modelos de aprendizaje automático mantener un equilibrio entre la complejidad y la robustez, asegurando un rendimiento óptimo en diversas aplicaciones.
 Campus
Campus