Funciones de Activación en Redes Neuronales
Las funciones de activación son componentes esenciales en las redes neuronales artificiales. Estas funciones determinan cómo se transforman las señales de entrada que llegan a una neurona en señales de salida. La elección de la función de activación adecuada puede tener un impacto significativo en la capacidad de la red para aprender y generalizar. En este texto, exploraremos los tipos más comunes de funciones de activación y discutiremos su importancia en la introducción de no linealidades en la red.
Tipos de Funciones de Activación
Existen varias funciones de activación utilizadas comúnmente en las redes neuronales. A continuación, se describen algunas de las más populares:
1. Función Sigmoide
- Descripción: La función sigmoide es una función no lineal que mapea cualquier valor de entrada a un rango entre 0 y 1. Su fórmula matemática es:
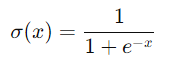
- Derivable, lo que facilita el cálculo del gradiente durante el entrenamiento.
- Comprime las entradas grandes a una salida cercana a 0 o 1, lo que puede ayudar a estabilizar la red.
2. ReLU (Rectified Linear Unit)
- Descripción: La función ReLU es una de las funciones de activación más utilizadas en la actualidad. Su fórmula es:
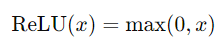
- Simple y eficiente en términos de cálculo.
- Introduce no linealidades sin saturarse para valores positivos.
- Puede causar "unidades muertas" cuando las neuronas quedan atrapadas en la parte negativa.
3. Función Tanh (Tangente Hipérbolica)
- Descripción: La función tanh es similar a la sigmoide, pero mapea los valores de entrada a un rango entre -1 y 1. Su fórmula es:
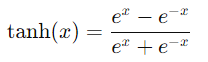
- Suave y continua.
- Derivable, similar a la sigmoide.
- Las salidas están centradas en cero, lo que puede ayudar a la convergencia durante el entrenamiento.
Importancia de las Funciones de Activación
Las funciones de activación son cruciales en las redes neuronales por varias razones:
1. Introducción de No Linealidades
- Necesidad de No Linealidades: Sin funciones de activación no lineales, una red neuronal con múltiples capas simplemente se comportaría como una transformación lineal, sin importar el número de capas. Esto limita severamente la capacidad de la red para modelar relaciones complejas en los datos.
- Capacidad de Representación: Las no linealidades permiten que la red neuronal aprenda y modele datos más complejos y patrones intrincados, aumentando su capacidad de representación y aproximación.
2. Propiedades de Aprendizaje
- Gradientes: Las funciones de activación como ReLU, sigmoide y tanh son derivables, lo que permite el uso del algoritmo de retropropagación para ajustar los pesos de la red durante el entrenamiento.
- Convergencia: La elección de una función de activación adecuada puede mejorar la velocidad de convergencia del entrenamiento y ayudar a evitar problemas como el desvanecimiento o explosión del gradiente.
3. Regularización
- Control de Saturación: Funciones como la sigmoide y tanh tienen regiones de saturación donde las derivadas se acercan a cero, lo que puede ayudar a regularizar la red y prevenir sobreajuste.
- Estabilidad Numérica: La función ReLU, aunque simple, ha demostrado ser efectiva en la práctica debido a su capacidad para mantener la estabilidad numérica y facilitar el entrenamiento de redes profundas.
En resumen, las funciones de activación son componentes vitales en las redes neuronales, permitiendo la introducción de no linealidades esenciales para el aprendizaje de patrones complejos y mejorando las propiedades de aprendizaje de la red. La selección y uso adecuado de estas funciones son cruciales para el éxito de los modelos de redes neuronales en diversas aplicaciones.
Enlace Adicional
Para màs información visite este sitio.
 Campus
Campus
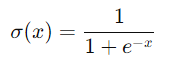
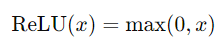
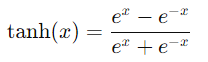 - Propiedades:
- Propiedades:
