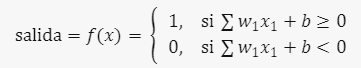Campus
Diagrama de temas
-
-
Introducción a las Redes Neuronales
Una red neuronal es un modelo computacional inspirado en la estructura y funcionamiento del cerebro humano. Estas redes son herramientas utilizadas en el campo de la inteligencia artificial (IA). Veamos algunos conceptos clave:
¿Qué es una red neuronal?
- Una red neuronal es un programa o modelo de machine learning que toma decisiones de manera similar al cerebro humano. Se basa en procesos que imitan la forma en que las neuronas biológicas trabajan juntas para identificar patrones, ponderar opciones y llegar a conclusiones.
- Cada red neuronal consta de capas de nodos o neuronas artificiales. Estas capas incluyen:
- Capa de entrada: Recibe datos iniciales.
- Capas ocultas: Pueden haber una o varias capas intermedias. Procesan y transforman la información.
- Capa de salida: Proporciona el resultado final.
- Cada nodo se conecta con otros nodos y tiene su propia ponderación y umbral asociados. Si la salida de un nodo supera el umbral, se activa y envía datos a la siguiente capa.
- Las redes neuronales se entrenan con datos para mejorar su precisión con el tiempo. Son fundamentales en informática e IA, permitiendo clasificar y agrupar datos rápidamente.
Conceptos fundamentales:
- Neuronas artificiales: Son unidades básicas en la red. Cada neurona procesa entradas y produce una salida.
- Estructura de la red neuronal: La organización de las neuronas en capas y sus conexiones determina cómo se procesa la información.
- Función de activación: Define la salida de una neurona según su entrada. Ejemplos incluyen la función sigmoide o ReLU (Rectified Linear Unit).
¿Cómo funcionan las redes neuronales?
Piensa en cada nodo individual como su propio modelo de regresión lineal, compuesto por datos de entrada, ponderaciones, un sesgo (umbral) y una salida. La fórmula sería:
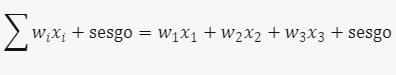
La salida se calcula como:
Una vez definida la capa de entrada, se asignan las ponderaciones. Estas ponderaciones determinan la importancia de cada variable. Luego, se multiplican las entradas por sus ponderaciones y se suman. La salida pasa por una función de activación y se envía a la siguiente capa.
En resumen, las redes neuronales son poderosas herramientas que permiten a las máquinas aprender y procesar información de manera similar a nuestro cerebro.
Enlace Adicionales
Para más información, visite este sitio.
-
Perceptrones
El perceptrón es un componente básico de las redes neuronales artificiales. Se inspira en las neuronas biológicas del cerebro humano y fue inventado por Frank Rosenblatt en 1958. Aunque es una simplificación, el perceptrón sigue un proceso similar al de una neurona real:
En términos geométricos, el límite de decisión de un perceptrón con 2 entradas es una línea. Si hay 3 entradas, el límite es un plano 2D. En general, con (n) entradas, el límite de decisión es un hiperplano que separa el espacio de características en dos partes: una para clasificación positiva y otra para clasificación negativa. El perceptrón es un clasificador binario lineal en función de sus pesos.1. Toma señales de entrada (denominadas (x_1, x_2, \ldots, x_n)).
2. Calcula una suma ponderada (z) de esas entradas.
3. Aplica una función de umbral (\phi) para emitir un resultado.
Para representarlo de manera vectorial, agrupamos todas las entradas ((x_0, x_1, \ldots, x_n)) y los pesos ((W_0, W_1, \ldots, W_n)) en vectores (x) y (w). La salida es 1 si el producto escalar es positivo y -1 en caso contrario.
Límites y Capacidades de los Perceptrones
- Linealmente Separables: El perceptrón solo puede clasificar correctamente si las clases son linealmente separables. Si los datos no se pueden separar mediante una línea recta (o hiperplano), el perceptrón no funcionará adecuadamente.
- Limitaciones: No puede resolver problemas más complejos que la separación lineal. Por ejemplo, no puede manejar funciones XOR.
- Capacidades: A pesar de sus limitaciones, el perceptrón es fundamental en el aprendizaje de máquinas y sentó las bases para modelos más avanzados, como las redes neuronales multicapa.
En resumen, el perceptrón es un modelo simple pero importante en el campo de la inteligencia artificial.Enlace Adicional
Para más información, visite este sitio.
-
Entrenamiento de Redes Neuronales
El entrenamiento de redes neuronales es un proceso crucial en el campo del aprendizaje automático y la inteligencia artificial. Este proceso permite a las redes neuronales aprender a realizar tareas específicas, como la clasificación de imágenes, el reconocimiento de voz o la predicción de series temporales, a partir de datos de entrenamiento. A través del ajuste de los pesos sinápticos internos, las redes neuronales pueden optimizar su rendimiento y minimizar los errores en sus predicciones. En este texto, exploraremos tres componentes fundamentales del entrenamiento de redes neuronales: el problema del aprendizaje supervisado, el algoritmo de retropropagación y la función de costo.
El Problema del Aprendizaje Supervisado
El aprendizaje supervisado es un tipo de aprendizaje automático en el cual una red neuronal es entrenada utilizando un conjunto de datos etiquetados. Cada dato en el conjunto de entrenamiento consiste en una entrada y una etiqueta correspondiente que representa el resultado deseado. El objetivo de la red es aprender una función que mapea las entradas a las salidas correctas. A continuación se describen los pasos del proceso de aprendizaje supervisado:
1. Recolección de Datos: Se compila un conjunto de datos de entrenamiento compuesto por pares de entrada y salida (x, y), donde x representa las características del dato y y es la etiqueta correspondiente.
2. Inicialización de la Red: Los pesos de las conexiones en la red neuronal se inicializan aleatoriamente.
3. Propagación hacia Adelante (Forward Propagation): Los datos de entrada se pasan a través de la red, capa por capa, hasta obtener una predicción de salida.
4. Cálculo del Error: Se calcula la diferencia entre la predicción de la red y la etiqueta verdadera utilizando una función de costo.
5. Ajuste de Pesos (Backpropagation): Se utilizan algoritmos de optimización para ajustar los pesos de la red de manera que el error se minimice.
Algoritmo de Retropropagación (Backpropagation)
El algoritmo de retropropagación es una técnica esencial utilizada para ajustar los pesos de la red neuronal durante el entrenamiento. Este algoritmo optimiza los pesos mediante el cálculo del gradiente de la función de costo con respecto a cada peso, y luego ajusta los pesos en la dirección opuesta a este gradiente. Los pasos del algoritmo de retropropagación son:
1. Propagación hacia Adelante: Como se describió anteriormente, los datos de entrada se pasan a través de la red para obtener la predicción de salida.
2. Cálculo del Error: Se calcula el error de predicción utilizando la función de costo.
3. Propagación hacia Atrás:
- Cálculo del Gradiente: Se calcula el gradiente de la función de costo con respecto a cada peso utilizando la regla de la cadena. Esto implica calcular las derivadas parciales de la función de costo con respecto a las salidas de cada nodo, luego con respecto a las entradas de cada nodo y finalmente con respecto a los pesos.
- Actualización de Pesos: Los pesos se ajustan en función del gradiente calculado y una tasa de aprendizaje, siguiendo la fórmula:
Función de Costo
La función de costo, también conocida como función de pérdida o error, es una medida que cuantifica el error entre las predicciones de la red neuronal y las etiquetas verdaderas del conjunto de datos de entrenamiento. El objetivo del entrenamiento es minimizar esta función de costo. Algunas funciones de costo comunes incluyen:
1. Error Cuadrático Medio (MSE):
2. Entropía Cruzada (Cross-Entropy):
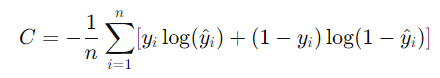
Esta función de costo es comúnmente utilizada en problemas de clasificación.
El uso de una función de costo adecuada es crucial para el éxito del entrenamiento de la red neuronal, ya que guía el proceso de optimización de los pesos hacia la minimización del error.
Estos componentes son fundamentales para entender cómo se entrenan las redes neuronales y cómo pueden aprender a realizar tareas específicas a partir de datos etiquetados.
Enlace Adicional
Para más información Consulte este sitio.
-
Funciones de Activación en Redes Neuronales
Las funciones de activación son componentes esenciales en las redes neuronales artificiales. Estas funciones determinan cómo se transforman las señales de entrada que llegan a una neurona en señales de salida. La elección de la función de activación adecuada puede tener un impacto significativo en la capacidad de la red para aprender y generalizar. En este texto, exploraremos los tipos más comunes de funciones de activación y discutiremos su importancia en la introducción de no linealidades en la red.
Tipos de Funciones de Activación
Existen varias funciones de activación utilizadas comúnmente en las redes neuronales. A continuación, se describen algunas de las más populares:
1. Función Sigmoide
- Descripción: La función sigmoide es una función no lineal que mapea cualquier valor de entrada a un rango entre 0 y 1. Su fórmula matemática es:
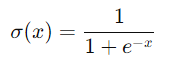
- Propiedades:
- Suave y continua.
- Derivable, lo que facilita el cálculo del gradiente durante el entrenamiento.
- Comprime las entradas grandes a una salida cercana a 0 o 1, lo que puede ayudar a estabilizar la red.
2. ReLU (Rectified Linear Unit)
- Descripción: La función ReLU es una de las funciones de activación más utilizadas en la actualidad. Su fórmula es:
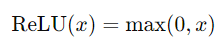
- Propiedades:
- Simple y eficiente en términos de cálculo.
- Introduce no linealidades sin saturarse para valores positivos.
- Puede causar "unidades muertas" cuando las neuronas quedan atrapadas en la parte negativa.
3. Función Tanh (Tangente Hipérbolica)
- Descripción: La función tanh es similar a la sigmoide, pero mapea los valores de entrada a un rango entre -1 y 1. Su fórmula es:
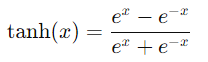- Propiedades:- Suave y continua.
- Derivable, similar a la sigmoide.
- Las salidas están centradas en cero, lo que puede ayudar a la convergencia durante el entrenamiento.Importancia de las Funciones de Activación
Las funciones de activación son cruciales en las redes neuronales por varias razones:
1. Introducción de No Linealidades- Necesidad de No Linealidades: Sin funciones de activación no lineales, una red neuronal con múltiples capas simplemente se comportaría como una transformación lineal, sin importar el número de capas. Esto limita severamente la capacidad de la red para modelar relaciones complejas en los datos.
- Capacidad de Representación: Las no linealidades permiten que la red neuronal aprenda y modele datos más complejos y patrones intrincados, aumentando su capacidad de representación y aproximación.
2. Propiedades de Aprendizaje
- Gradientes: Las funciones de activación como ReLU, sigmoide y tanh son derivables, lo que permite el uso del algoritmo de retropropagación para ajustar los pesos de la red durante el entrenamiento.
- Convergencia: La elección de una función de activación adecuada puede mejorar la velocidad de convergencia del entrenamiento y ayudar a evitar problemas como el desvanecimiento o explosión del gradiente.
3. Regularización
- Control de Saturación: Funciones como la sigmoide y tanh tienen regiones de saturación donde las derivadas se acercan a cero, lo que puede ayudar a regularizar la red y prevenir sobreajuste.
- Estabilidad Numérica: La función ReLU, aunque simple, ha demostrado ser efectiva en la práctica debido a su capacidad para mantener la estabilidad numérica y facilitar el entrenamiento de redes profundas.
En resumen, las funciones de activación son componentes vitales en las redes neuronales, permitiendo la introducción de no linealidades esenciales para el aprendizaje de patrones complejos y mejorando las propiedades de aprendizaje de la red. La selección y uso adecuado de estas funciones son cruciales para el éxito de los modelos de redes neuronales en diversas aplicaciones.
Enlace Adicional
Para màs información visite este sitio.
-
Redes Neuronales Multicapa (MLP)
Las Redes Neuronales Multicapa, conocidas como MLP (Multilayer Perceptron), son un tipo fundamental de redes neuronales artificiales ampliamente utilizadas en el aprendizaje automático. Estas redes se caracterizan por su capacidad de aprender representaciones complejas de los datos mediante la utilización de múltiples capas de neuronas. En este texto, exploraremos la estructura de las MLP y el proceso de propagación hacia adelante, que es crucial para el cálculo de la salida de la red a partir de una entrada dada.
Estructura de las Redes Neuronales Multicapa (MLP)
Las MLP están compuestas por varias capas de neuronas que trabajan juntas para procesar y transformar los datos de entrada en salidas útiles. A continuación se describe la estructura de una MLP típica:
1. Capa de Entrada: Esta es la primera capa de la red y se encarga de recibir los datos de entrada. Cada neurona en la capa de entrada representa una característica del dato de entrada. Por ejemplo, en una red que procesa imágenes, cada píxel de la imagen puede ser una entrada.
2. Capas Ocultas: Las capas ocultas son las que se encuentran entre la capa de entrada y la capa de salida. Estas capas son responsables de realizar transformaciones complejas en los datos de entrada mediante la aplicación de funciones de activación no lineales. Las MLP pueden tener una o varias capas ocultas, y cada capa adicional aumenta la capacidad de la red para aprender representaciones más complejas.
- Neurona: Cada neurona en una capa oculta recibe una combinación ponderada de las salidas de las neuronas de la capa anterior.
- Pesos y Biases: Las conexiones entre las neuronas de diferentes capas están asociadas con pesos, y cada neurona tiene un bias que se suma antes de aplicar la función de activación.
3. Capa de Salida: La última capa de la red es la capa de salida, que produce la salida final de la MLP. El número de neuronas en la capa de salida depende del tipo de problema que se esté resolviendo. Por ejemplo, en un problema de clasificación binaria, habría una neurona de salida, mientras que en una clasificación multiclase, habría tantas neuronas como clases.
Propagación hacia Adelante
La propagación hacia adelante es el proceso mediante el cual una MLP calcula su salida a partir de una entrada dada. Este proceso implica pasar los datos de entrada a través de todas las capas de la red hasta obtener la salida final. Aquí se describe el proceso en detalle:
1. Cálculo en la Capa de Entrada: Los datos de entrada x se introducen en la red. Cada neurona de la capa de entrada simplemente pasa su valor a la primera capa oculta.
2. Cálculo en las Capas Ocultas:
- Suma Ponderada: Cada neurona en una capa oculta recibe entradas xi de las neuronas de la capa anterior y calcula una suma ponderada:
- Función de Activación: La suma ponderada zj se pasa a través de una función de activación para producir la salida de la neurona j:
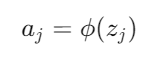
3. Cálculo en la Capa de Salida: El proceso se repite para todas las capas ocultas hasta llegar a la capa de salida. En la capa de salida, las neuronas realizan el mismo cálculo de suma ponderada y aplicación de la función de activación para producir la salida final de la red y.
Importancia de la Estructura y la Propagación hacia Adelante
La estructura de las MLP con múltiples capas ocultas permite a la red aprender características jerárquicas y representaciones complejas de los datos, lo que es crucial para tareas como la clasificación de imágenes, el procesamiento del lenguaje natural y muchos otros problemas de aprendizaje automático. El proceso de propagación hacia adelante es fundamental para la predicción, ya que determina cómo los datos de entrada se transforman en la salida de la red, permitiendo así el aprendizaje y la generalización a partir de ejemplos vistos durante el entrenamiento.
Enlace Adicional
Para más información, consulte este sitio.
-
Regularización en Redes Neuronales
La regularización es una técnica crucial en el entrenamiento de redes neuronales que ayuda a prevenir el sobreajuste (overfitting) y mejorar la capacidad de generalización del modelo. El sobreajuste ocurre cuando un modelo se ajusta demasiado a los datos de entrenamiento, capturando el ruido y las particularidades del conjunto de datos específico en lugar de aprender patrones generalizables. Para abordar este problema, se utilizan varios métodos de regularización que penalizan la complejidad del modelo. En este texto, exploraremos algunos de los métodos de regularización más comunes, como el Dropout y la regularización L2, y discutiremos la importancia de la regularización para mejorar la generalización del modelo.
Métodos de Regularización
1. Dropout
- Descripción: Dropout es una técnica de regularización en la que, durante el entrenamiento, se eliminan aleatoriamente (se ponen a cero) un porcentaje de las unidades (neuronas) de la red en cada iteración. Esto impide que las neuronas dependan demasiado unas de otras y fuerza a la red a aprender representaciones más robustas y generalizables.
- Implementación: En cada paso de entrenamiento, cada neurona tiene una probabilidad 𝑝 de ser "apagada". Durante la fase de prueba, todas las neuronas están activas, pero sus salidas se escalonan por el factor 𝑝 para mantener la consistencia en las magnitudes de las salidas.
- Ventajas: Dropout es efectivo en la reducción del sobreajuste y es fácil de implementar. Además, introduce un tipo de ensemblado de redes neuronales durante el entrenamiento, lo que mejora la robustez del modelo.
2. Regularización L2 (Penalización de Peso)
- Descripción: La regularización L2, también conocida como decaimiento de peso, añade una penalización al error de la función de costo basada en la magnitud de los pesos de la red. La idea es evitar que los pesos se vuelvan demasiado grandes, lo que puede llevar a un modelo más complejo y propenso al sobreajuste.
- Fórmula: La función de costo con regularización L2 se define como:
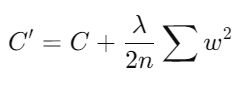
donde C es la función de costo original, λ es el parámetro de regularización que controla la fuerza de la penalización, n es el número de ejemplos de entrenamiento, y w son los pesos de la red.
- Ventajas: La regularización L2 ayuda a mantener los pesos pequeños, promoviendo un modelo más simple y menos propenso al sobreajuste. Es particularmente útil en modelos con muchas características o parámetros.
Importancia de la Regularización
La regularización juega un papel fundamental en la mejora de la generalización de los modelos de redes neuronales por varias razones:
1. Prevención del Sobreajuste: Al penalizar la complejidad del modelo y evitar que los pesos crezcan demasiado, la regularización ayuda a que el modelo no se ajuste demasiado a los datos de entrenamiento. Esto es esencial para que el modelo pueda generalizar bien a nuevos datos no vistos durante el entrenamiento.
2. Mejora de la Robustez del Modelo: Técnicas como Dropout introducen un grado de aleatoriedad durante el entrenamiento, lo que fuerza a la red a aprender representaciones más robustas y menos dependientes de combinaciones específicas de neuronas.
3. Reducción de la Varianza: La regularización puede ayudar a reducir la varianza del modelo, haciendo que sus predicciones sean más estables y menos sensibles a pequeñas variaciones en los datos de entrada.
4. Promoción de la Simplicidad del Modelo: Al imponer una penalización sobre la magnitud de los pesos, la regularización fomenta modelos más simples que tienden a ser más interpretables y a tener mejor rendimiento en datos no vistos.
En conclusión, la regularización es una técnica vital para el entrenamiento efectivo de redes neuronales, ya que ayuda a prevenir el sobreajuste y mejora la capacidad de generalización del modelo. Métodos como Dropout y la regularización L2 son herramientas poderosas que permiten a los modelos de aprendizaje automático mantener un equilibrio entre la complejidad y la robustez, asegurando un rendimiento óptimo en diversas aplicaciones.
-
Optimización en Redes Neuronales
La optimización es un proceso esencial en el entrenamiento de redes neuronales, cuyo objetivo es ajustar los parámetros del modelo (principalmente los pesos y biases) para minimizar la función de costo. Existen varios métodos de optimización que se utilizan para este propósito, cada uno con sus propias ventajas y desventajas. Además, el ajuste adecuado de los hiperparámetros es crucial para mejorar el rendimiento del modelo. En este texto, exploraremos algunos de los métodos de optimización más comunes y proporcionaremos una guía sobre cómo seleccionar y ajustar los hiperparámetros.
Métodos de Optimización
1. Gradiente Descendente Estocástico (SGD)- Descripción: El Gradiente Descendente Estocástico es una variante del gradiente descendente que actualiza los pesos del modelo utilizando un solo ejemplo de entrenamiento a la vez. Esto introduce ruido en el proceso de actualización, lo que puede ayudar a escapar de los mínimos locales.
- Fórmula de Actualización:
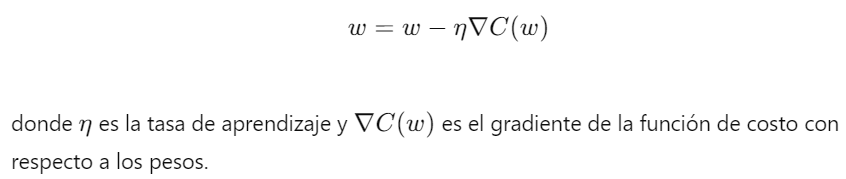
- Ventajas: SGD es simple y eficiente en términos de memoria, y puede converger más rápido que el gradiente descendente batch para grandes conjuntos de datos.
- Desventajas: La actualización ruidosa puede dificultar la convergencia y provocar oscilaciones alrededor del mínimo.
2. Adam (Adaptive Moment Estimation)
- Descripción: Adam es un método de optimización que combina las ventajas de dos técnicas: AdaGrad y RMSProp. Utiliza estimaciones adaptativas de momentos de primer y segundo orden.
- Fórmulas de Actualización:
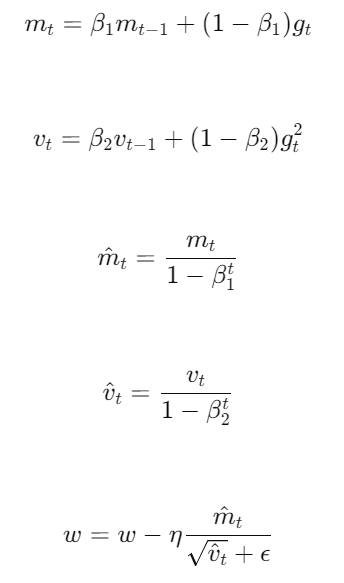
donde es el gradiente en el tiempo y son los estimados de primer y segundo momento, es la tasa de aprendizaje, y son parámetros de decaimiento exponencial, y es un término de estabilidad numérica.
- Ventajas: Adam es robusto y eficiente en términos de memoria, y generalmente funciona bien en una amplia variedad de problemas.
- Desventajas: Puede ser sensible a la configuración de hiperparámetros y, en algunos casos, puede no generalizar tan bien como SGD.3. Otros Métodos de Optimización
- RMSProp: Similar a AdaGrad, pero con un decaimiento exponencial de los gradientes pasados. Es útil para problemas donde la tasa de aprendizaje decreciente de AdaGrad es demasiado agresiva.
- AdaGrad: Ajusta la tasa de aprendizaje para cada parámetro, haciéndola más pequeña a medida que aumenta el número de actualizaciones. Es útil para características esparsas pero puede resultar en tasas de aprendizaje demasiado pequeñas.
- Momentum: Añade un término que acumula las actualizaciones pasadas, lo que ayuda a acelerar la convergencia en la dirección correcta y a reducir las oscilaciones.
Ajuste de Hiperparámetros
El ajuste de hiperparámetros es crucial para mejorar el rendimiento de una red neuronal. Aquí se presentan algunas estrategias para seleccionar y ajustar los hiperparámetros:
1. Tasa de Aprendizaje ():- Importancia: Controla la magnitud de las actualizaciones de los pesos. Una tasa de aprendizaje demasiado alta puede provocar divergencia, mientras que una demasiado baja puede hacer que el modelo tarde mucho en converger.- Ajuste: Comenzar con valores estándar (como 0.01) y ajustar gradualmente mediante validación cruzada.2. Tamaño del Batch:- Importancia: Afecta la estabilidad y la eficiencia del entrenamiento. Batches más grandes proporcionan estimaciones del gradiente más precisas, pero requieren más memoria.- Ajuste: Experimentar con diferentes tamaños de batch (como 32, 64, 128) y evaluar su impacto en la velocidad de convergencia y la precisión.3. Número de Épocas:- Importancia: Determina cuántas veces el modelo verá el conjunto de entrenamiento completo. Un número insuficiente de épocas puede resultar en un modelo infraajustado, mientras que demasiadas épocas pueden llevar al sobreajuste.- Ajuste: Utilizar la validación cruzada para detener el entrenamiento cuando el rendimiento en el conjunto de validación comience a empeorar.4. Parámetros Específicos de los Optimizadores:- Adam (): Valores típicos son y .
- Momentum: Un valor común es 0.9, pero puede ser ajustado según el problema.
Regularización (Dropout, L2):- Dropout Rate: Generalmente se establece entre 0.2 y 0.5.- Factor de Regularización L2 (): Un valor pequeño (como 0.0001) es un buen punto de partida, ajustándolo según el rendimiento de validación.Importancia del Ajuste de Hiperparámetros
El ajuste de hiperparámetros es crucial para maximizar el rendimiento del modelo y evitar problemas como el sobreajuste o el infraajuste. Un ajuste adecuado de los hiperparámetros puede mejorar significativamente la precisión y la capacidad de generalización del modelo, haciendo que sea más robusto y eficiente en una variedad de tareas y conjuntos de datos.
Enlace Adicional
Para más información acceda a este sitio.
-
Redes Neuronales Convolucionales (CNN)
Las Redes Neuronales Convolucionales (CNN, por sus siglas en inglés) son una clase especial de redes neuronales diseñadas específicamente para procesar datos con una estructura de cuadrícula, como las imágenes. Las CNN han revolucionado el campo de la visión por computadora debido a su capacidad para capturar patrones espaciales y jerárquicos en las imágenes. Estas redes son ampliamente utilizadas en tareas como el reconocimiento de objetos, la segmentación de imágenes y la detección de rostros, entre otras aplicaciones.
Fundamentos de las Redes Neuronales Convolucionales (CNN)
Las CNN se inspiran en la organización de la corteza visual del cerebro humano y están diseñadas para procesar y reconocer patrones visuales directamente a partir de los datos en bruto. A continuación, se describen los componentes fundamentales y el funcionamiento de las CNN:
1. Estructura de las CNN: Una CNN típica está compuesta por una serie de capas, incluyendo capas convolucionales, capas de pooling (submuestreo) y capas completamente conectadas (fully connected). La combinación de estas capas permite a la red aprender representaciones jerárquicas de los datos de entrada.
2. Aprendizaje de Características: Las capas convolucionales actúan como detectores de características locales, capturando patrones simples como bordes y texturas en las primeras capas, y patrones más complejos como formas y objetos en capas más profundas.
3. Invariancia a Traslaciones: Gracias a la operación de pooling, las CNN pueden lograr invariancia a pequeñas traslaciones y distorsiones en los datos de entrada, lo que mejora la robustez del modelo.
Capas Convolucionales y de Pooling
Las capas convolucionales y de pooling son los componentes clave que permiten a las CNN procesar eficientemente los datos visuales.
Capas Convolucionales
1. Operación de Convolución: La operación de convolución es el núcleo de las capas convolucionales. Consiste en aplicar un filtro (también llamado kernel) sobre la entrada para producir un mapa de características. Matemáticamente, la convolución de una entrada I con un filtro K se expresa como:
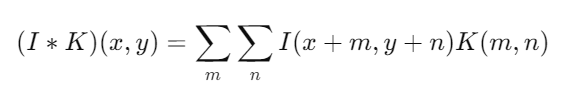
2. Mapas de Características: El resultado de la convolución es un conjunto de mapas de características que resaltan las activaciones del filtro en diferentes regiones de la imagen. Cada filtro aprende a detectar una característica específica.
3. Parámetros de la Convolución: Los parámetros importantes en la operación de convolución incluyen el tamaño del filtro, el stride (paso), que determina cuánto se desplaza el filtro sobre la entrada, y el padding (relleno), que controla cómo se manejan los bordes de la entrada.
Capas de Pooling
1. Operación de Pooling: La operación de pooling reduce la dimensionalidad de los mapas de características y retiene la información más importante. La técnica más común es el max-pooling, que selecciona el valor máximo en una ventana de tamaño fijo.
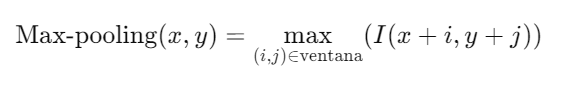
2. Propósito del Pooling: El pooling reduce la cantidad de parámetros y el costo computacional, además de proporcionar invariancia a pequeñas traslaciones en la entrada.
3. Tipos de Pooling: Además del max-pooling, otro tipo común es el average-pooling, que toma el promedio de los valores en la ventana de pooling.
Aplicaciones en Visión por Computadora
Las CNN han demostrado ser extremadamente eficaces en una variedad de tareas de visión por computadora, incluyendo:
1. Reconocimiento de Objetos: Identificación y clasificación de objetos dentro de imágenes.
2. Segmentación de Imágenes: División de una imagen en segmentos o regiones significativas.
3. Detección de Rostros: Localización y reconocimiento de rostros en imágenes y videos.
4. Análisis de Videos: Procesamiento de secuencias de imágenes para tareas como la detección de movimiento y el seguimiento de objetos.
En resumen, las Redes Neuronales Convolucionales (CNN) son una poderosa herramienta en el campo de la visión por computadora, gracias a su capacidad para aprender y reconocer patrones complejos en los datos visuales. Las operaciones de convolución y pooling permiten a las CNN extraer características jerárquicas e invariantes, lo que mejora significativamente su rendimiento en diversas aplicaciones.
-
Redes Neuronales Recurrentes (RNN)
Las Redes Neuronales Recurrentes (RNN, por sus siglas en inglés) son una clase de redes neuronales diseñadas para manejar datos secuenciales, como series temporales, texto y datos de audio. A diferencia de las redes neuronales tradicionales, las RNN tienen conexiones recurrentes que permiten que la información persista, lo que las hace especialmente adecuadas para tareas donde el contexto y el orden de los datos son importantes. En este texto, exploraremos la estructura de las RNN y discutiremos algunos de los problemas comunes que enfrentan, como el desvanecimiento y el estallido del gradiente.
Estructura de las Redes Neuronales Recurrentes (RNN)
Las RNN están diseñadas para procesar secuencias de datos mediante la introducción de ciclos en la red que crean dependencias temporales. A continuación, se describen los componentes y el funcionamiento de las RNN:
1. Neurona Recurrente: A diferencia de las neuronas en las redes neuronales tradicionales, cada neurona en una RNN no solo recibe la entrada actual, sino también su propia salida anterior. Esto permite que la red mantenga un estado interno que puede capturar información a lo largo de la secuencia.
2. Estructura de la RNN: La estructura básica de una RNN se puede describir mediante la siguiente ecuación:
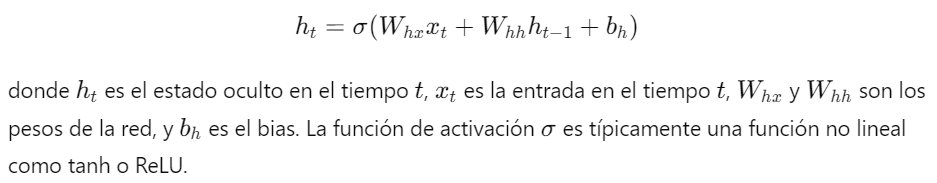
3. Salida de la RNN: La salida de la red en cada tiempo puede estar dada por:
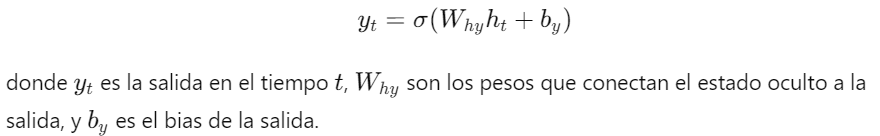
4. Backpropagation Through Time (BPTT): Para entrenar una RNN, se utiliza una variación del algoritmo de retropropagación llamada retropropagación a través del tiempo. Este algoritmo extiende el cálculo del gradiente a lo largo de toda la secuencia temporal.
Problemas Comunes en las RNN
Aunque las RNN son poderosas para manejar datos secuenciales, enfrentan varios desafíos durante el entrenamiento, entre los que destacan el desvanecimiento del gradiente y el estallido del gradiente.
1. Desvanecimiento del Gradiente (Vanishing Gradient):
- Descripción: El desvanecimiento del gradiente ocurre cuando los gradientes de la función de pérdida con respecto a los pesos se vuelven extremadamente pequeños a medida que se propagan hacia atrás en el tiempo. Esto puede hacer que las actualizaciones de los pesos sean insignificantes, impidiendo que la red aprenda dependencias a largo plazo.
- Causas: El uso de funciones de activación como la sigmoide o tanh puede exacerbar este problema debido a sus derivadas que se acercan a cero en sus extremos.
2. Estallido del Gradiente (Exploding Gradient):
- Descripción: El estallido del gradiente ocurre cuando los gradientes se vuelven extremadamente grandes durante la retropropagación. Esto puede hacer que los pesos se actualicen de manera abrupta, llevando a inestabilidad en el entrenamiento y posibles divergencias.
- Causas: Este problema es común cuando los gradientes se multiplican repetidamente a lo largo de muchas capas, lo que puede suceder en secuencias largas.
Soluciones a los Problemas de Gradiente
1. Uso de Funciones de Activación Adecuadas: El uso de funciones de activación como ReLU puede ayudar a mitigar el problema del desvanecimiento del gradiente.
2. Regularización y Normalización: Técnicas como la normalización por lotes (batch normalization) pueden ayudar a mantener los gradientes en un rango adecuado.
3. Clipping de Gradientes: El clipping de gradientes es una técnica que limita el tamaño de los gradientes para prevenir el estallido del gradiente. Consiste en establecer un umbral máximo para los gradientes y escalar los gradientes que exceden este umbral.
4. Redes LSTM y GRU: Las arquitecturas avanzadas como LSTM (Long Short-Term Memory) y GRU (Gated Recurrent Unit) están diseñadas específicamente para manejar el problema del desvanecimiento del gradiente al introducir puertas que controlan el flujo de información a través de la red.
En resumen, las Redes Neuronales Recurrentes (RNN) son una herramienta poderosa para procesar datos secuenciales, pero enfrentan desafíos significativos como el desvanecimiento y el estallido del gradiente. Comprender y abordar estos problemas es crucial para el entrenamiento efectivo de RNNs y para aprovechar todo su potencial en diversas aplicaciones de secuencias de datos.
-
Aplicaciones Prácticas de las Redes Neuronales
Las redes neuronales artificiales han revolucionado numerosas áreas de la tecnología y la ciencia mediante su capacidad para aprender y generalizar a partir de datos. Estas redes, inspiradas en el cerebro humano, pueden modelar relaciones complejas y descubrir patrones en datos masivos, lo que las hace ideales para una amplia gama de aplicaciones prácticas. En este texto, exploraremos algunas de las aplicaciones más impactantes de las redes neuronales en la vida real, centrándonos en el reconocimiento de imágenes y el procesamiento del lenguaje natural.
Aplicaciones en la Vida Real
1. Reconocimiento de Imágenes
El reconocimiento de imágenes es una de las áreas más destacadas donde las redes neuronales, especialmente las Redes Neuronales Convolucionales (CNN), han demostrado un rendimiento sobresaliente. A continuación, se presentan algunas aplicaciones específicas:
- Detección de Objetos: Las CNN se utilizan para identificar y localizar objetos en imágenes y videos. Aplicaciones prácticas incluyen la vigilancia de seguridad, donde las cámaras pueden detectar automáticamente actividades sospechosas, y los vehículos autónomos, que utilizan la detección de objetos para identificar señales de tráfico, peatones y otros vehículos.
- Reconocimiento Facial: Las redes neuronales permiten el reconocimiento preciso de rostros humanos, lo cual se utiliza en sistemas de seguridad y autenticación biométrica, como los desbloqueos de teléfonos móviles y el control de acceso en edificios seguros.
- Diagnóstico Médico: En el campo de la medicina, las CNN se aplican para analizar imágenes médicas como radiografías, resonancias magnéticas y tomografías. Estas redes pueden ayudar a los médicos a detectar enfermedades como el cáncer, las enfermedades cardíacas y las anomalías cerebrales con alta precisión.
2. Procesamiento de Lenguaje Natural (NLP)
El procesamiento de lenguaje natural es otra área donde las redes neuronales, especialmente las Redes Neuronales Recurrentes (RNN) y los Transformadores, han tenido un impacto significativo. Algunas aplicaciones clave incluyen:
- Traducción Automática: Las redes neuronales se utilizan para traducir texto de un idioma a otro. Servicios como Google Translate emplean modelos avanzados de redes neuronales para proporcionar traducciones precisas y coherentes en tiempo real.
- Asistentes Virtuales: Los asistentes virtuales como Siri, Alexa y Google Assistant utilizan redes neuronales para comprender y responder a las consultas de los usuarios. Estos sistemas pueden realizar tareas como enviar mensajes, configurar recordatorios y proporcionar información sobre el clima y las noticias.
- Análisis de Sentimiento: Las redes neuronales se utilizan para analizar el sentimiento en textos escritos, como reseñas de productos, publicaciones en redes sociales y comentarios de clientes. Esto es útil para empresas que desean comprender mejor las opiniones y emociones de sus clientes.
3. Otros Ejemplos de Aplicaciones
- Sistemas de Recomendación: Plataformas como Netflix, Amazon y Spotify utilizan redes neuronales para recomendar productos, películas, música y otros contenidos a los usuarios, basándose en sus preferencias y comportamientos anteriores.
- Juego y Entretenimiento: Las redes neuronales se aplican en el desarrollo de inteligencia artificial para videojuegos, permitiendo a los personajes del juego comportarse de manera realista y adaptativa. Además, se utilizan en la creación de contenido generativo, como la música y el arte.
- Control de Calidad en Manufactura: En la industria manufacturera, las redes neuronales se utilizan para inspeccionar productos en la línea de producción, identificando defectos y garantizando altos estándares de calidad.
Importancia de las Aplicaciones Prácticas
Las aplicaciones prácticas de las redes neuronales no solo demuestran su versatilidad y potencia, sino que también destacan su impacto en mejorar la eficiencia, precisión y capacidad de los sistemas tecnológicos. Desde la mejora de la atención médica hasta la transformación de la interacción humano-computadora, las redes neuronales continúan impulsando innovaciones que benefician a la sociedad en múltiples niveles.
-
Avances y Tendencias en Redes Neuronales
Las redes neuronales y el aprendizaje profundo (deep learning) han experimentado avances significativos en los últimos años, impulsados por el desarrollo de nuevas arquitecturas y técnicas. Estos avances han permitido abordar problemas complejos y mejorar el rendimiento en diversas aplicaciones. En este texto, exploraremos algunas de las arquitecturas avanzadas más destacadas, como los Transformers y las Redes Generativas Antagónicas (GAN), así como las tendencias futuras en la investigación de redes neuronales y deep learning.
Nuevas Arquitecturas y Técnicas
Transformers
1. Descripción: Los Transformers son una arquitectura de red neuronal que ha revolucionado el procesamiento del lenguaje natural (NLP). Introducidos por Vaswani et al. en 2017, los Transformers utilizan mecanismos de atención para procesar secuencias de datos, lo que permite capturar relaciones a largo plazo de manera más eficiente que los modelos recurrentes tradicionales.
- Mecanismo de Atención: El componente clave de los Transformers es el mecanismo de atención, que asigna pesos a diferentes partes de la entrada, permitiendo al modelo enfocarse en las partes más relevantes para la tarea.
- Ventajas: Los Transformers han demostrado ser altamente eficaces en tareas de traducción automática, generación de texto y otras aplicaciones de NLP debido a su capacidad para manejar dependencias largas y procesar datos en paralelo.2. Aplicaciones: Los Transformers se utilizan en modelos de lenguaje avanzados como BERT, GPT y T5, que han establecido nuevos estándares en tareas de comprensión y generación de lenguaje natural.
Redes Generativas Antagónicas (GAN)
1. Descripción: Las Redes Generativas Antagónicas (GAN) son una clase de modelos generativos introducidos por Ian Goodfellow en 2014. Las GAN consisten en dos redes neuronales, un generador y un discriminador, que compiten entre sí.
- Generador: La red generadora crea datos falsos similares a los datos reales.
- Discriminador: La red discriminadora evalúa si los datos provienen del conjunto de datos real o del generador.
- Entrenamiento: Durante el entrenamiento, el generador y el discriminador se mejoran mutuamente: el generador intenta producir datos más realistas, mientras que el discriminador se vuelve más preciso en la detección de datos falsos.
2. Aplicaciones: Las GAN se utilizan en una amplia gama de aplicaciones, incluyendo la generación de imágenes realistas, el super-resolución de imágenes, la transferencia de estilo y la creación de datos sintéticos para entrenar otros modelos.
Tendencias Futuras en Redes Neuronales y Deep Learning
Investigación en Modelos de Gran Escala
1. Modelos Preentrenados de Gran Escala: La tendencia hacia el uso de modelos preentrenados de gran escala, como GPT-3, muestra que los modelos más grandes y con más datos pueden capturar mejor las complejidades del lenguaje y otros tipos de datos. Estos modelos se utilizan como base para una variedad de tareas mediante el ajuste fino (fine-tuning) en conjuntos de datos específicos.
2. Transferencia de Aprendizaje: La transferencia de aprendizaje sigue siendo una tendencia importante, permitiendo a los modelos aprovechar el conocimiento adquirido en una tarea para mejorar el rendimiento en otra tarea relacionada.
Mejora de la Eficiencia y Sostenibilidad
1. Modelos más Eficientes: La investigación se centra en desarrollar modelos más eficientes en términos de computación y energía, lo que es crucial para aplicaciones prácticas y sostenibles. Técnicas como la compresión de modelos, la cuantización y los modelos ligeros (lightweight models) están ganando popularidad.
2. Sostenibilidad y Green AI: La sostenibilidad en la investigación de IA está ganando atención, con un enfoque en reducir la huella de carbono de los entrenamientos de modelos grandes y promover prácticas de investigación más ecológicas.
Interpretabilidad y Explicabilidad
1. Interpretabilidad de Modelos: La interpretabilidad de los modelos de deep learning es una área de investigación creciente, con el objetivo de hacer que las decisiones de los modelos sean más comprensibles para los humanos. Esto es especialmente importante en aplicaciones críticas como la salud y la justicia.
2. Explicabilidad: Las técnicas de explicabilidad buscan proporcionar explicaciones claras y comprensibles de cómo y por qué un modelo toma decisiones específicas, lo que es crucial para la confianza y la adopción en entornos del mundo real.
Conclusión
Los avances en arquitecturas como los Transformers y las GAN han llevado a mejoras significativas en diversas aplicaciones de redes neuronales y deep learning. Al mismo tiempo, las tendencias futuras en este campo se centran en la creación de modelos más grandes y eficientes, mejorar la sostenibilidad y la interpretabilidad, y explorar nuevas aplicaciones y técnicas que continúen empujando los límites de lo que es posible con la inteligencia artificial.
-
Campus
