 Campus
Campus
Diagrama de temas
-
-
Clasificación binaria
La clasificación es la tarea de colocar ejemplos de datos en categorías, y el tipo más simple de clasificación es la clasificación binaria. En la clasificación binaria, se determina que un ejemplo de datos es un 1 o un 0. O es algo, o no lo es. Está activado o desactivado. Existe o no existe. En otras palabras, solo hay dos opciones.
Los esquemas de clasificación binaria son frecuentes en campos como el cuidado de la salud, donde los profesionales médicos se benefician de diagnosticar a un paciente como si tuviera alguna afección (1) o no la tuviera (0). Por ejemplo, un clasificador binario podría diagnosticar a un paciente como con una cardiopatía con base en una serie de características, y el clasificador podría hacerlo más rápidamente o con más precisión que un médico humano. Otra área donde la clasificación binaria sobresale es en la predicción de equipos defectuosos. Ciertos equipos pueden mostrar signos de falla inminente, por lo que un clasificador binario podría determinar si algo está a punto de fallar (1) o no (0). Hay muchos ejemplos de la utilidad de la clasificación binaria. Existen varios algoritmos que realizan la clasificación binaria. El primero que aprenderá es la regresión logística. -
Regresión logística
La regresión logística es un tipo de análisis de regresión en el que la salida es una probabilidad de clasificación entre 0 y 1. El análisis de regresión es la técnica de identificación de las relaciones entre variables. La regresión logística es uno de los algoritmos de aprendizaje automático más comunes que se usan en la clasificación porque puede producir resultados con relativa rapidez en conjuntos de datos más grandes.
El término regresión logística puede ser algo confuso. Aunque, desde el punto de vista técnico, es un tipo de análisis de regresión, la regresión logística se utiliza con más frecuencia para tareas de clasificación. Cuando los profesionales de la ciencia de datos y el aprendizaje automático usan el término general "regresión", por lo general, se refieren a la tarea de estimar las relaciones entre las variables continuas y generar una estimación que también es un valor continuo. Por ejemplo, predecir el valor monetario de una casa es un tipo de tarea de regresión: no está poniendo nada en categorías. Un algoritmo como la regresión lineal se puede utilizar para resolver este problema porque genera valores continuos. Por otro lado, la regresión logística se puede utilizar para colocar los datos en categorías, por lo que normalmente se trata como una tarea de clasificación.
El valor que genera un algoritmo de regresión logística se denomina función logística. Este es un tipo de función sigmoidea porque tiene forma de S, como se muestra aquí.
Figura 1. Una función sigmoidea empleada en la regresión logística. 
En la situación que se muestra en el gráfico, trata de predecir si alguien recomendará o no un nuevo videojuego a otras personas después de haberlo jugado. Una de las características que determina esto es la "calificación del jugador", que el jugador proporciona como parte de una encuesta de fin de juego. Observe que la función es capaz de ajustarse al valor atípico en la parte superior derecha, y que al hacerlo, toma una forma de S. Si la función fuera una línea recta (como en la regresión lineal), no sería capaz de ajustar este valor atípico de manera limpia.
La función logística se puede expresar como la siguiente ecuación:

Donde:
- t es la estimación entre infinito negativo e infinito positivo.
- e es la base natural del logaritmo.
El valor de estimación (es decir, el valor estimado por la función logística) está entre 0 y 1. La meta de la función logística es estimar los parámetros del modelo, los valores que el modelo "aprende" para mejorar sus capacidades de toma de decisiones.
Información adicional
Para obtener más información sobre la regresión logística, consulte este sitio.
-
Límite de decisión
En un problema de clasificación, la línea de división que separa las clases negativas de las positivas es el límite de decisión. Esto determina a qué clase pertenece un ejemplo en función del valor que estima entre 0 y 1. Un límite de decisión se puede expresar como las siguientes instrucciones, donde
p̂es el valor de estimación eŷes la clasificación:
Nota: Observe el uso del símbolo “sombrero” por encima de
yyp. Este símbolo se utiliza a menudo para denotar una estimación de un modelo.
Por lo tanto, si el modelo calcula un valor de estimación mayor o igual que 0,50, entonces clasifica esa instancia como un 1 (recomendará el juego). Si el valor de estimación es menor que 0,50, el modelo clasifica la instancia como 0 (no recomendará el juego). Cuando se grafica en una función sigmoidea, esto tendría un aspecto similar al siguiente:Figura 1. Una función sigmoidea aplicada a un problema de clasificación. Tenga en cuenta que el límite de decisión en este caso se seleccionó arbitrariamente. 
El límite de decisión en una función sigmoidea es capaz de tener en cuenta el valor atípico, lo que mejora la capacidad del algoritmo para clasificar los ejemplos de datos. Puede configurar un límite diferente en función de los datos y el contexto del problema que está intentando resolver. Un límite de decisión de 0,50 no siempre es la mejor opción posible.
-
Clasificación multietiqueta
El ejemplo de regresión logística dado anteriormente funciona con una opción binaria simple: algo es x, o no es x. O un jugador recomendará el juego, o no lo hará. Sin embargo, es posible que se enfrente a un problema de clasificación que implica varias etiquetas, también denominada clasificación multietiqueta. Por ejemplo, supongamos que desea obtener más información sobre el rendimiento de los equipos deportivos. Necesita varias formas de clasificar el rendimiento de cada equipo (una fila) en un juego o partido. En este caso, el modelo de aprendizaje automático debe clasificar lo siguiente para cada equipo:
- Categoría 1: si el equipo está en el equipo local o en el equipo visitante.
- Categoría 2: si el equipo ganó o perdió el partido.
El equipo es el equipo local o el equipo visitante, y no puede ser ambos. Del mismo modo, suponiendo que no se permitan empates, el equipo ganó o perdió. Aunque las clases de cada categoría se excluyen mutuamente, no ocurre lo mismo entre las categorías. Usted puede estar en el equipo local ganador, el equipo visitante ganador, el equipo local perdedor o el equipo visitante perdedor. Son cuatro posibles etiquetas de clasificación.Puede resolver problemas de varias etiquetas entrenando varios modelos de clasificación binarios, a menos que las propias etiquetas estén correlacionadas. Puede entrenar dos modelos (uno para la categoría 1 y el otro para la categoría 2) y, a continuación, combinar los resultados. -
Clasificación multiclase
La clasificación multiclase es el proceso de colocar un ejemplo de datos dentro de una sola clase entre tres o más opciones. Esto difiere de la clasificación de varias etiquetas en que las clases son mutuamente excluyentes. Un ejemplo no puede pertenecer a la clase A, B y C; debe pertenecer a A o B o C.
En el ejemplo de deportes, puede desglosar los partidos en el tipo de deporte que se está jugando:
- Fútbol americano
- Baloncesto
- Béisbol
- Y así sucesivamente...El juego es fútbol americano o algunos deportes que no lo son; no puede ser ambas cosas. A diferencia de los problemas multietiqueta, los problemas multiclase requieren un enfoque diferente al de combinar clasificadores binarios. Este enfoque se denomina regresión logística multinomial y genera probabilidades para cada clase que suman 1. Por lo tanto, si un equipo anotó 42 puntos totales y jugó durante un tiempo total de 3,5 horas, la salida podría ser:
Así, el algoritmo determina que el juego es de fútbol. Y, como se puede ver, todos los porcentajes suman 1 (100 %).- 89 % fútbol americano.
- 8 % baloncesto.
- 3 % béisbol.
Nota: También es posible tener un problema multietiqueta y multiclase. Por ejemplo, la categoría 2 en el ejemplo anterior podría incluir vínculos, lo que significaría que hay tres etiquetas posibles para esa clase. -
Mecánica del entrenamiento de un modelo
Antes de pasar al siguiente algoritmo de clasificación, es posible que se pregunte cómo los profesionales entrenan modelos a partir de algoritmos. Los pasos previos al entrenamiento, así como los pasos posteriores, requieren mucha reflexión y toma de decisiones. Obtener los mejores resultados posibles es, en muchos casos, un proceso complicado. Sin embargo, la mecánica real de entrenamiento de un modelo es bastante simple en la mayoría de los conjuntos de herramientas de aprendizaje automático.
La mecánica de entrenamiento de un modelo usando un lenguaje de programación como Python® se puede resumir de la siguiente manera:
1. El profesional introduce datos de entrenamiento en una función de programación para un algoritmo en particular.
2. El algoritmo realiza cálculos en función de los datos y, a continuación, cuando termina, genera un modelo.
3. El profesional aplica el modelo como quiere, como probar el modelo o hacer una predicción sobre nuevos datos.
Los cálculos del algoritmo ocurren detrás de escena, por lo que un profesional no necesita ajustar manualmente los datos en una fórmula. A pesar de que el profesional no está realmente haciendo nada en el paso 2, un computador sí lo está haciendo, y según varios factores; este paso de entrenamiento puede llevar al computador a cualquier momento, desde microsegundos hasta meses.
-
Entrenamiento y ajuste de modelos de regresión logística
Archivos de datos
/home/student/ITSAI/Classification/Classification.ipynb
/home/student/ITSAI/Classification/data/train.csvAntes de empezar
La máquina virtual y Jupyter® Notebook no están abiertos.
Escenario
Se le dio un conjunto de datos sobre uno de los desastres más conocidos de la historia: el hundimiento del RMS Titanic. Haya múltiples factores que pueden haber influido en quién sobrevivió y quién no. Usted quiere poder llegar a sus propias conclusiones y verificar esas conclusiones a través de la experiencia práctica. Por lo tanto, decide crear un modelo de aprendizaje automático que le ayudará a lograr eso.
Utilizará un conjunto de datos del mundo real que incluye varias estadísticas sobre los pasajeros del Titanic. La etiqueta en este caso es si el pasajero sobrevivió o no. Por lo tanto, entrenará varios modelos de clasificación, comenzando con el algoritmo de regresión logística, que intentará predecir quién sobrevivió y quién no. En última instancia, desea poder alimentar el modelo con sus propios datos, por ejemplo, usted y sus amigos podrían ser "pasajeros" con sus propias características (edad, sexo, número de hermanos, etc.), para que pueda determinar si usted sobreviviría o no al desastre.
-------------------------------------------------------------------------------------------------------------------------------------------------------------
1. Inicie el entorno de actividad.
-------------------------------------------------------------------------------------------------------------------------------------------------------------1. En el escritorio, haga doble clic en la aplicación Oracle VM VirtualBox para iniciarla.
2. En Oracle VM VirtualBox Manager, en la lista de la izquierda, seleccione ITSAI y, a continuación, 2. seleccione Computador→Inicio→Inicio normal.
3. Espere a que se inicie el sistema operativo.
2. Inicie Jupyter Notebook.
-------------------------------------------------------------------------------------------------------------------------------------------------------------1. En el escritorio, haga doble clic en el icono de Jupyter para iniciar el servidor de Jupyter Notebook y abrir un explorador web.
2. Seleccione ITSAI.
3. Seleccione Clasificación.
4. Seleccione Classification.ipynb para abrirlo.
3. Importe las bibliotecas relevantes y cargue el conjunto de datos.
1. Desplácese hacia abajo y vea la celda titulada Importar bibliotecas de software y cargue el conjunto de datos y examine la lista de código debajo de ella.

Este código importa las diversas bibliotecas de software que se utilizarán en este programa.
2. Ejecute la celda de código.
3. Compruebe que newdata.csv y train.csv están en la carpeta del proyecto y que este último se cargó con 891 registros.

Se proporcionan entrenamientos independientes y nuevos conjuntos de datos. El archivo train.csv es un conjunto de datos etiquetado que se va a usar para entrenar los modelos. El archivo newdata.csv es un conjunto de datos sin etiqueta que contiene datos para los que desea que el modelo tome decisiones de clasificación. Dividirá el conjunto de datos de entrenamiento para crear también un conjunto de validación. Primero, deberá familiarizarse con los datos.
Nota: Ya se realizó algún preprocesamiento en este conjunto de datos para ingresar algunos valores que faltan, codificar valores, combinar algunas características y quitar columnas que no serán necesarias en los modelos.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------4. Familiarícese con los datos.
1. Desplácese hacia abajo y vea la celda titulada Familiarizarse con el conjunto de datos y examine la lista de código debajo de ella.

Este código generará los distintos tipos de datos incluidos en el conjunto de datos.
2. Ejecute la celda de código.
3. Examine el resultado.

- El conjunto de entrenamiento incluye 891 filas y 10 columnas.
- 8 columnas contienen valores enteros y 2 contienen valores flotantes.
- Todas las columnas tienen un valor en cada fila.
- Varias columnas no necesitan explicación, pero esta es la descripción de las que sí la necesitan:
-Survived con un valor de 0 significa que el pasajero no sobrevivió; 1 significa sí lo hizo. Esta es la etiqueta de mayor importancia.
-Pclass es la clase de boleto. En otras palabras, un valor de 1 significa que el pasajero viajaba en primera clase, el servicio más caro y de mayor calidad. Esto también actúa como un indicador de la situación socioeconómica del pasajero.
-SibSp se refiere al número de hermanos más un cónyuge que el pasajero tenía a bordo.
-Parch se refiere al número de padres e hijos que el pasajero tenía a bordo.
-Fare es el costo del boleto del pasajero, que probablemente se correlaciona con Pclass.
-SizeOfFamily es la combinación de SibSp y Parch para obtener el número total de pasajeros para el boleto.
-SexEncoding es el valor numérico codificado para el género del pasajero: 1 para mujer y 2 para hombre.
-EmbarkedEncoding es el valor numérico codificado que hace referencia al puerto desde donde se embarcó el pasajero: 1 para Southampton, 2 para Cherburgo y 3 para Queenstown.
-TitleEncoding es el valor numérico codificado que indica si un pasajero tiene un título personal: 1 para Sr., 2 para Sra., etc.
4. En la siguiente celda de código, examine el código.

Este código mostrará las primeras 5 filas del conjunto de datos.
5. Ejecute la celda de código.6. Examine el resultado.
 -------------------------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------------------------Todos los valores son numéricos. Nuevamente, estos datos fueron preparados de antemano.
5. Examine un resumen general de las estadísticas.
1. Desplácese hacia abajo y vea la celda titulada Examinar un resumen general de las estadísticas y examine la lista de código debajo de ella.

Este código generará estadísticas generales para las columnas con valores numéricos en el conjunto de datos.
2. Ejecute la celda de código.
3. Examine el resultado.

- La media para
Survivedes 0,38. Dado que las entidades de esta columna contienen un 1 (sobrevivió) o un 0 (no sobrevivió), esto significa que el 38 % de los pasajeros del conjunto de entrenamiento sobrevivieron.- El valor
Agemínimo muestra que el pasajero más joven del conjunto tenía menos de un año (0,42). El valorAgemáximo era de 80 años.- La edad media era de
29.36años.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------6. Teniendo en cuenta lo que sabe sobre el conjunto de datos hasta el momento, ¿Qué características cree que podrían influir en las tasas de supervivencia?
------------------------------------------------------------------------------------------------------------------------------------------------------------------------7. Utilice la visualización de barras apiladas para mostrar los números de supervivencia.
1. Desplácese hacia abajo y vea la celda titulada Usar visualización de barras apiladas para mostrar los números de supervivencia y examine la lista de código debajo de ella.

Este código generará gráficos de barras apiladas para las columnas
Pclass,SexEncoding,SizeOfFamilyyEmbarkedEncoding.2. Ejecute la celda de código.
3. Examine el resultado.
 ------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------- Para cada fila de gráficos, el número de pasajeros que perecieron se muestra en la barra de la izquierda y el número de pasajeros que sobrevivieron se muestra en la barra de la derecha.
- En general, los pasajeros tenían más probabilidades de perecer que de sobrevivir.
- La mayoría de las personas que perecieron estaban en tercera clase. Sin embargo, tenga en cuenta que estos gráficos miden valores absolutos y no proporciones. Puede haber habido más personas en tercera clase que en cualquier otra clase.
- La mayoría de las personas que perecieron eran hombres (2).
- La mayoría de las personas que perecieron no estaban con sus familiares.
- Las personas que se embarcaron desde Cherburgo (2) tenían más probabilidades de sobrevivir que de perecer.
- Las personas que se embarcaron desde Southampton (1) tenían más probabilidades de perecer que de sobrevivir.
8. Busque relaciones entre supervivencia, edad y sexo.
1. Desplácese hacia abajo y vea la celda titulada Buscar relaciones entre supervivencia, edad y sexo y examine la lista de código que aparece debajo de ella.

Este código generará gráficos de barras apiladas por
SexEncodingyAgeque muestran el número de sobrevivientes para cada una.2. Ejecute la celda de código.
3. Examine el resultado.

Como era de esperar, las pasajeras tuvieron tasas de supervivencia más altas que los pasajeros masculinos. Del mismo modo, menos de los ancianos sobrevivieron en comparación con los pasajeros más jóvenes, aunque esto es más obvio para los pasajeros masculinos que para los femeninos.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------9. Divida los conjuntos de datos.
1. Desplácese hacia abajo y vea la celda titulada Dividir los conjuntos de datos y examine la lista de código debajo de ella.

Este código dividirá el conjunto de datos en conjuntos de entrenamiento y de validación.
2. Ejecute la celda de código.
3. Examine el resultado.

El conjunto de datos de entrenamiento original se dividió en dos: un conjunto para seguir usándolo como conjunto de entrenamiento y otro para usarlo como conjunto de validación. Tenga en cuenta que la etiqueta
Survivedse quitó de las matricesXy se colocó en su propio vectory.------------------------------------------------------------------------------------------------------------------------------------------------------------------------Nota:
X_train/val/testyy_train/val/testes un esquema de nomenclatura convencional para las divisiones de conjuntos de datos en el aprendizaje automático. A veces, los profesionales utilizarán variables más descriptivas en su lugar.10. Cree un modelo de regresión logística.
1. Desplácese hacia abajo y vea la celda titulada Crear un modelo de regresión logística y examine la lista de código que aparece debajo de ella.

- Este código creará un modelo de regresión logística y mostrará el tiempo que se tardó en generar y la puntuación del modelo.
- La línea 3 es lo que crea el modelo usando scikit-learn. En este caso, especifica tres hiperparámetros diferentes y sus valores:
- solver = 'sag'
- C = 0.05
- max_iter = 10000
- Estos hiperparámetros se eligieron arbitrariamente. Estas pueden no ser las mejores opciones posibles, como verá en breve.
- No es necesario que entienda exactamente lo que significan estos hiperparámetros. Basta con saber que cambian la forma en que el algoritmo de regresión logística aprende de los datos de entrenamiento, así como la forma en que intenta evitar el sobreajuste.
2. Ejecute la celda de código.
3. Examine el resultado.

La puntuación para este modelo es de alrededor del 79 %. Tenga en cuenta que la puntuación predeterminada para un modelo de clasificación en scikit-learn es la precisión. Obtendrá más información sobre la precisión y otras métricas de clasificación en el tema siguiente. Por ahora, solo considere que una puntuación más alta es más deseable.
4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo de regresión logística para predecir la supervivencia de los pasajeros en el conjunto de validación.
5. Ejecute la celda de código.
6. Examine el resultado.

Además de las columnas existentes, la clasificación predicha por el modelo en el conjunto de validación se compara con el valor de etiqueta real. Las probabilidades de cada clasificación también se muestran en las columnas más a la derecha. Estas probabilidades son los resultados que la función de regresión logística genera y utiliza para determinar qué clase predecir. Por ejemplo, si
ProbPerishedes mayor queProbSurvived, entonces el modelo habrá predicho un 0 para ese pasajero en particular (es decir, no sobrevivió).Nota: Quizás deba desplazarse hacia la derecha para ver todos los valores de probabilidad. Para ello, haga clic y arrastre la barra de desplazamiento en la parte inferior de la tabla.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------11. Ajuste un modelo de regresión logística.
1. Desplácese hacia abajo y vea la celda titulada Ajustar un modelo de regresión logística y examine la lista de código que aparece debajo de ella.

Este código básicamente realiza los mismos pasos de entrenamiento que antes. La diferencia es que, en la línea 1, se configuran diferentes hiperparámetros:
- solveres ahora'liblinear'.- Ces ahora0.10.- Se agregó
penalty = 'l2'como un nuevo hiperparámetro.- max_itersigue siendo10000.2. Ejecute la celda de código.
3. Examine el resultado.

La puntuación de este modelo mejoró del 79 % al 83 % después del ajuste.
4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo de regresión logística ajustado para predecir la supervivencia de los pasajeros en el conjunto de validación.
5. Ejecute la celda de código.
6. Examine el resultado.

Como puede ver, las predicciones y las probabilidades de predicción para cada pasajero son algo diferentes del modelo de regresión logística no ajustado original. Por ejemplo, en la cuarta fila, el modelo ajustado predijo correctamente que el pasajero sobrevivió, mientras que el modelo original no lo hizo.
-
k vecino más cercano (k-NN)
El algoritmo k vecino más cercano (k-NN) es un enfoque de clasificación alternativo en el que un ejemplo de datos se coloca en una clase en función de sus similitudes con otros ejemplos de datos. Estas similitudes se derivan del espacio de características (es decir, la combinación de todas las características de entrenamiento). Por ejemplo, desea clasificar un cuerpo de agua como un lago o un océano. Si un cuerpo de agua es más grande por superficie y profundidad máxima, es más similar a los cuerpos de agua etiquetados como océanos que a los etiquetados como lagos. Por lo tanto,
k-NN clasificará el ejemplo como un océano.
Nota: También puede ver
k-NN abreviado como KNN.
Lakenk-NN define el número de ejemplos de datos que son los vecinos más cercanos del ejemplo en cuestión. “Más cercano” en este caso se refiere a la distancia entre los puntos de datos cuando se asignan al espacio de la característica. Mediantek,k-NN realiza una votación de estos puntos vecinos para determinar cómo clasificar el ejemplo en cuestión. En la siguiente figura,k = 3, por lo que el algoritmo toma un voto de los tres vecinos más cercanos al ejemplo de datos (la X verde). Dado que dos de los tres vecinos están en la clase 0 (círculos azules oscuros), el ejemplo de datos se clasifica como 0 (lago).Figura 1. Clasificación k-NN donde k = 3. 
En comparación con la regresión logística,
k-NN es más fácil de implementar porque en realidad no “aprende” de la misma manera que los algoritmos de aprendizaje automático típicos; en otras palabras, no mejora su capacidad de clasificación a través del entrenamiento. También genera una clasificación directamente en lugar de una probabilidad (es decir, genera un 0 o 1). Sin embargo,k-NN puede tardar mucho tiempo en calcular las clasificaciones de los conjuntos de datos grandes, por lo que se prefiere la regresión logística en esos casos.Nota:
k-NN también puede resolver problemas de regresión, pero se utiliza con mayor frecuencia en la clasificación.Información adicional
Para obtener más información sobre
k-NN, consulte este sitio.
-
Determinación de k
Al igual que muchos hiperparámetros en el aprendizaje automático, la elección de
kenk-NN depende en última instancia de la naturaleza de los datos de entrenamiento y la salida que está buscando. No hay necesariamente un valor perfecto paraken todas las circunstancias conocidas. Cuanto más grande seak, menos “ruidoso” se vuelve el conjunto de datos con respecto a la clasificación; en otras palabras, se reduce el efecto de anomalías o ejemplos mal etiquetados. Sin embargo, esto también conduce a límites menos distintos entre las clases, y puede aumentar el costo computacional. Los valores más bajos dekson mejores para mantener estos límites distintos, pero son menos efectivos para minimizar el efecto del ruido en los datos.Consulte el siguiente ejemplo. En la figura, el valor de
kde antes (3) se ha ajustado a un nuevo valor (5) en el mismo conjunto de entrenamiento. El modelo ahora clasifica el ejemplo como un 1 (océano) en lugar de un 0 (lago) porque hay más votos de 1 (triángulos azul claro) que votos de 0 entre los cinco vecinos más cercanos. Un cambio dekcomo este puede cambiar totalmente la clasificación que recibe un ejemplo de datos.Figura 1. Cambiar k en un modelo k-NN puede conducir a resultados diferentes. 
Una regla general a la hora de seleccionar
kes hacer queksea siempre impar cuando se tiene un problema de clasificación binaria; esto elimina la posibilidad de que haya un empate en la votación. Otro enfoque para seleccionarkse denomina bootstrapping e implica tomar la raíz cuadrada del número total de ejemplos de datos en el conjunto de entrenamiento. El valor resultante es aproximadamente lakque debe considerar usar. También puede utilizar una técnica de prueba de rendimiento como la validación cruzada para ayudar a determinar un valor aceptable parak. -
Entrenamiento y ajuste de modelos k-NN
Antes de empezar
Classification-Boston.ipynb está abierto en Jupyter Notebook.
Nota: Si cerró Jupyter Notebook desde que completó la actividad anterior, deberá reiniciar Jupyter Notebook y volver a abrir el archivo. Para asegurarse de que todos los objetos y la salida de Python están en el estado correcto para comenzar esta actividad:
- Seleccione Kernel→Reiniciar & y Borrar salida.
- Seleccione Reiniciar y borrar todas las salidas.
- Desplácese hacia abajo y seleccione la celda con la etiqueta Crear un modelo k vecinos más cercanos.
- Seleccione Celda→ Ejecutar todo lo anterior.
Escenario
Ahora que entrenó y ajustó los modelos de regresión logística, puede hacer lo mismo con el algoritmo
kvecinos más cercanos. No hay, necesariamente, un mejor algoritmo para el problema en cuestión, por lo que es una buena idea experimentar siempre que sea posible.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------1.Cree un modelo k vecinos más cercanos.
1. Desplácese hacia abajo y vea la celda titulada Crear un modelo k vecinos más cercanos y examine la lista de código que aparece debajo de ella.

Este código creará un modelo
kvecinos más cercanos y mostrará el tiempo que se tardó en generar y la puntuación del modelo.2. Ejecute la celda de código.
3. Examine el resultado.

- Es una alternativa al modelo de regresión logística creado en el paso anterior. Ambos modelos realizan una clasificación binaria, pero es útil crear varios modelos para ver si uno funciona mejor que otro.
- La puntuación para el modelo
kvecinos más cercanos es de alrededor del 75 %. Esto parece tener un rendimiento más bajo que el modelo de regresión logística, por lo que utilizará el modelo de regresión logística para el conjunto de pruebas real.- En este caso,
kse genera mediante un método de bootstrapping, tomando la raíz cuadrada del número total de ejemplos de datos en el conjunto de entrenamiento. Para ayudar a evitar votos de empate en un clasificador binario,kse incrementa por 1 si es par.4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo
kvecinos más cercanos para predecir la supervivencia de los pasajeros.5. Ejecute la celda de código.
6. Examine el resultado.

La información incluida aquí está en el mismo formato que los resultados del modelo de regresión logística anterior, pero las predicciones son diferentes debido al modelo diferente utilizado.
Nota: Dado que
k-NN no genera probabilidades de predicción de la misma manera que lo hace la regresión logística, el métodopredict_proba()muestra la fracción de vecinos que votaron por cada etiqueta. Así, en la primera fila de resultados, el ~93 % de los vecinos votaron por pereció (25 de un total de 27).------------------------------------------------------------------------------------------------------------------------------------------------------------------------2.Ajuste un modelo k vecinos más cercanos.
1. Desplácese hacia abajo y vea la celda titulada Ajustar un modelo k vecinos más cercanos y examine la lista de código que aparece debajo de ella.

Este código volverá a crear el modelo
kvecinos más cercanos utilizando un valor de hiperparámetro diferente parak(n_neighbors). En este caso, el valor que era27ahora se incrementa por 10 a37.2. Ejecute la celda de código.
3. Examine el resultado.

La puntuación de este modelo empeoró del 75 % al 71 % después del ajuste. Cambiar los hiperparámetros no siempre da como resultado un modelo mejor.
4. En la siguiente celda de código, examine el código.
 5. Ejecute la celda de código.
5. Ejecute la celda de código.Este código utilizará el modelo
k-NN ajustado para predecir la supervivencia de los pasajeros en el conjunto de validación.6. Examine el resultado.
 Al igual que con el modelo de regresión logística, el ajuste del modelo
Al igual que con el modelo de regresión logística, el ajuste del modelok-NN produjo resultados diferentes. Por ejemplo, en la tercera fila, el modelo ajustado predijo incorrectamente que el pasajero sobrevivió, mientras que el modelo original no lo hizo. -
Máquinas de vectores de soporte (SVM)
Las máquinas de vectores de soporte (SVM) son algoritmos de aprendizaje supervisado que se pueden utilizar para resolver problemas de clasificación y regresión. Los SVM separan los valores de datos mediante un hiperplano. El hiperplano incluye un límite de decisión que es una función de línea o curva. A cada lado de este límite hay una función de línea o curva que es paralela y equidistante al límite de decisión. Estas funciones se denominan márgenes de vectores de soporte. Las funciones en cualquiera de los bordes de estos márgenes son los vectores de soporte.
Es mucho más fácil comprender el concepto de SVM mediante el uso de elementos visuales, así que considere la siguiente figura, en la que un hiperplano se traza en un gráfico.
Figura 1. Un ejemplo de un hiperplano usado en SVM. 
-
SVM para clasificación lineal
Cómo se construye un hiperplano y cómo se aplica a los datos dependen del tipo de problema de aprendizaje automático que está intentando resolver. La figura anterior demostró un hiperplano aplicado a un problema de clasificación lineal; es decir, un problema de clasificación cuyas clases se pueden dividir razonablemente utilizando una línea recta cuando se asignan a un espacio de características.
En la ilustración siguiente, el gráfico de la izquierda muestra un límite de decisión mediante un algoritmo de clasificación lineal estándar. El límite de decisión en este gráfico hace un buen trabajo al separar ambas clases en el espacio de características, pero se acerca mucho a los ejemplos de datos de borde. Esto probablemente dará lugar a problemas de sobreajuste, ya que los nuevos datos de prueba pueden no generalizarse bien utilizando este modelo. Compare esto con el modelo introducido anteriormente (a la derecha de esta figura), que utiliza SVM. El límite de decisión se traza de tal manera que no solo divide las clases, sino que permanece lo más lejos posible de los ejemplos de borde. Las líneas discontinuas crean los márgenes de separación intersectando los ejemplos de arista.
Figura 1. Un clasificador lineal sin SVM (izquierda) en comparación con un clasificador lineal con SVM (derecha). 
Ahora, observe lo que sucede cuando se evalúa un nuevo ejemplo de prueba en el modelo.
Figura 2. Clasificación de un ejemplo de prueba para un modelo sin SVM (izquierda) y un modelo con SVM (derecha). 
Aunque el ejemplo de prueba tiene los mismos valores cuando se conecta a ambos modelos, el modelo con SVM lo clasificó de manera diferente. Por lo tanto, las SVM son útiles en tareas de clasificación en las que los datos de entrenamiento incluyen valores atípicos. Tienden a superar la regresión logística y otros algoritmos de clasificación en este sentido. Sin embargo, cuando se usan SVM, es muy importante escalar los datos, más que en otros algoritmos de clasificación. Si una característica tiene valores mucho más grandes que otra, tendrá una influencia indebida en las distancias que se calculan entre los vectores de soporte y el límite de decisión. La distribución de los puntos de datos es más importante en este caso que el rango de cada característica.
Nota: Las SVM también pueden resolver problemas de clasificación no lineal, pero una discusión de esto está más allá del ámbito de este curso.
Información adicional
Para obtener más información sobre los SVM, consulte este sitio. -
Clasificación Naïve Bayes
La clasificación Naïve Bayes es otro tipo de algoritmo de clasificación utilizado en el aprendizaje automático. Calcula las probabilidades de clasificación basadas en el teorema de Bayes, que, cuando se aplica a un problema de clasificación, se puede representar como:
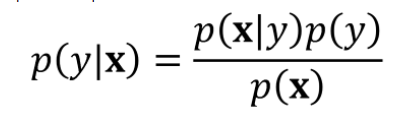
Donde:
- y es la clasificación observada.
- x es un vector (una matriz unidimensional) de las características del conjunto de datos.
- p(y|x) es la probabilidad de y dada x. También se llama la probabilidad posterior. Esto es lo que está tratando de determinar.
- p(x|y) es la probabilidad de x dada y.
- p(y) es la probabilidad de y independiente de las características. También se llama la probabilidad anterior.
- p(x) es la probabilidad de x independiente de la clase.
El “ingenuo” en la clasificación Naïve Bayes se refiere al hecho de que las probabilidades se calculan con la suposición de que las características son condicionalmente independientes. En otras palabras, una característica no interactúa con otra. Si su conjunto de datos de encuesta de videojuegos tuviera campos como “Tiempo de reproducción” y “Partidos jugados”, no sería adecuado para la clasificación Naïve Bayes, ya que es probable que esas dos variables se influyan entre sí. En la práctica, es raro que un problema de aprendizaje automático o sus conjuntos de datos incluyan solo características independientes. Sin embargo, si se encuentra con una tarea de este tipo, los clasificadores Naïve Bayes pueden superar significativamente la regresión logística tanto en el tiempo de entrenamiento como en la habilidad del modelo.
Una de las aplicaciones más comunes del mundo real de la clasificación Naïve Bayes es en el filtrado de spam. Los filtros de spam pueden analizar el texto de los correos electrónicos para que cada componente textual (por ejemplo, una palabra o frase) se analice independientemente de los demás. La presencia de ciertas palabras o frases puede solicitar al modelo que clasifique un mensaje de correo electrónico como “spam” o “no spam”, independientemente de cómo aparezcan estas palabras o frases en un contexto más amplio. Además, los clasificadores Naïve Bayes han encontrado éxito en el análisis de sentimientos, como determinar si los usuarios están satisfechos con un producto o servicio basado en el contenido de sus publicaciones en redes sociales.
Información adicional
Para obtener más información sobre la clasificación Naïve Bayes, consulte este sitio.
-
Árbol de decisión
Otro algoritmo que puede realizar la clasificación es un árbol de decisión. Un árbol de decisión es una disposición de las declaraciones condicionales y sus conclusiones en una estructura rama-hoja. Considere la siguiente figura, en la que está intentando determinar si un nuevo jugador recomendará o no su videojuego a otros usuarios.
Figura 1. Un árbol de decisión que determina si un jugador recomendará o no un juego. 
Un árbol de decisión se parece a un diagrama de flujo, donde cada “rama” representa una decisión basada en alguna condición y cada “hoja” representa una salida. Los nodos de decisión reciben la entrada en función de decisiones anteriores hasta que esa rama concreta termina en una hoja.
En este ejemplo, los rectángulos son los nodos de decisión y los óvalos son los valores de salida. Los valores de salida en este caso son etiquetas de clasificación. Las decisiones son “Sí” o “No”. Cualquier ejemplo de datos (un jugador) debe comenzar en el nodo de decisión raíz (clasificación del jugador). Si el jugador le ha dado al juego una calificación baja, el modelo predice inmediatamente que no lo recomendará. Si el jugador no le da al juego una calificación baja, pasa al siguiente nodo (tiempo de juego). Si han jugado más de 100 minutos en su sesión, el modelo predice que recomendarán el juego. Si el jugador no juega durante tanto tiempo, continúa hasta el nodo de decisión final (edad). Si tienen menos de 24 años, el modelo predice que darán una recomendación. Si tienen menos de 24 años, el modelo predice que no darán una recomendación. En última instancia, cualquier ejemplo de datos que se somete a este árbol de decisión recibirá una clasificación basada en sus características.
Los árboles de decisión se usan ampliamente en el aprendizaje automático porque son fáciles de entender y no requieren tanta preparación de datos como algunos otros algoritmos. Esto se debe a que la estructura del árbol de decisión será la misma en un conjunto de datos, independientemente de los procedimientos como el escalado o la ingeniería de características que aplique.
Nota: Los árboles de decisión no solo son capaces de clasificación, sino también de tareas de regresión.
-
Árbol de clasificación y regresión (CART)
El algoritmo de árbol de clasificación y regresión (CART) es uno de los algoritmos de árbol de decisión más populares en el aprendizaje automático. CART utiliza el índice de Gini como una métrica para construir el árbol de decisión a partir del conjunto de datos de entrenamiento. El algoritmo divide el conjunto de entrenamiento en dos basado en una sola característica con un valor de umbral. Por ejemplo, primero dividirá el conjunto de datos en función de la característica “Clasificación del jugador” y elegirá un valor de decisión, en este caso mayor que 4. Realiza esta elección mediante el uso de la función de costo de índice de Gini para determinar la “pureza” del nodo de decisión. El nodo de decisión más puro es aquel en el que todos los ejemplos de datos en el nodo de decisión pertenecen a una clase y ninguno pertenece a la otra. El nodo de decisión más impuro es aquel en el que los ejemplos de datos se dividen entre 50 y 50 entre cada clase.
La siguiente es la fórmula para el índice de Gini:
Donde:
- pies la probabilidad de que un ejemplo de datos se ubique en la clasei, mediante una única característica y la etiqueta.
- ces el número total de clases.El índice de Gini se calcula para cada valor de una característica, luego se toma una suma ponderada para que esos valores produzcan el índice de Gini definitivo para una característica. Este proceso se repite para el resto de las características del conjunto de datos. La característica con el nivel más alto de pureza (
G = 0), y por lo tanto el índice de Gini más bajo, se elige como el nodo de decisión raíz.Nota: En el contexto de la división del árbol de decisión, el nombre “índice de Gini” es una referencia a una medida de la desigualdad de ingresos, similarmente llamada índice de Gini. También se conoce como el coeficiente de Gini. Lleva el nombre de Corrado Gini, el estadístico que desarrolló la medición de la desigualdad.
Información adicional
Para obtener más información sobre CART, consulte este sitio.
-
Hiperparámetros de CART
Los siguientes son algunos de los principales hiperparámetros asociados con CART.
Hiperparámetro Descripción max_depthUtilice esto para especificar qué tan “profundo” debe ir el árbol, es decir, el número de nodos de decisión de la raíz a la salida más lejana, que se relaciona con el número de veces que se dividen los datos. Si no especifica una profundidad máxima, CART seguirá dividiendo el conjunto de datos hasta que
G(pureza) de todas las salidas sea 0, o hasta que todos los nodos de decisión sean menores que el valor demin_samples_split.En su búsqueda por lograr altos niveles de pureza de decisión, los árboles de decisión tienden a ser víctimas del sobreajuste, especialmente cuando el conjunto de datos tiene muchas características. El parámetro
max_depthes una forma de regularizar el entrenamiento para evitar el sobreajuste. No hay necesariamente un valor de profundidad ideal para todos los escenarios; debe evaluar el rendimiento del modelo para determinar el valor ideal para su tarea específica.min_samples_splitUtilice esta opción para especificar cuántas muestras (por ejemplo, ejemplos de datos) son necesarias para dividir un nodo de decisión. Al aumentar este valor, se restringe el modelo porque cada nodo debe contener muchos ejemplos antes de que se pueda dividir. Esto puede ayudar a minimizar el sobreajuste, pero restringir demasiado el modelo puede conducir a un ajuste insuficiente. min_samples_leafUtilícelo para especificar cuántas muestras deben estar en un nodo de salida. Una vez más, aumentar este valor puede reducir el sobreajuste, pero también tiene la oportunidad de conducir a un ajuste insuficiente.
Nota: Los nombres exactos de los parámetros pueden diferir en función de la biblioteca de programación utilizada; los nombres de la tabla anterior se basan en scikit-learn, la biblioteca principal de aprendizaje automático para Python.
-
Aprendizaje de conjuntos
El aprendizaje de conjuntos es una aplicación de aprendizaje automático en el que las estimaciones de varios modelos se consideran juntas. El objetivo es obtener una estimación más hábil de la que obtendría cualquier modelo de forma aislada. Aunque un único modelo entrenado con un conjunto específico de hiperparámetros puede parecer que resuelve un problema de clasificación o regresión, no es necesariamente la forma óptima de resolver el problema. Los estudios han demostrado que la agregación de estimaciones de múltiples modelos, especialmente un conjunto diverso de modelos, tiende a conducir a mejores estimaciones.
Por ejemplo, puede entrenar varios modelos en el problema de la encuesta de videojuegos. Uno de los modelos se puede entrenar mediante una regresión logística; otro podría ser entrenado usando Bayes ingenuo; otro utilizando un árbol de decisión; y así sucesivamente. Cada modelo puede alcanzar un cierto nivel de habilidad, dependiendo de cómo mida esa habilidad. Simplemente elegir el modelo que tiene lo mejor de cualquier medición de habilidad no le garantiza resultados ideales. En su lugar, muchos métodos de aprendizaje de conjuntos utilizan un sistema de votación por mayoría que selecciona la clase que está determinada por la mayoría de los modelos. Por ejemplo, los siguientes modelos determinan un clasificador binario para el problema de los videojuegos:
- Modelo de regresión logística- Exactitud: 78%
- Estimación: Clase 1
- Modelo bayesiano ingenuo
- Exactitud: 86%
- Estimación: Clase 0
- Modelo CART
- Exactitud: 81%
- Estimación: Clase 1
Por lo tanto, el método de conjunto determinaría la clase 1 porque es la mayoría. A pesar de que el modelo que bayesiano ingenuo tenía la mayor precisión, su estimación de 0 no se considera tan útil como el voto mayoritario. Esto puede parecer contraintuitivo, pero considere cómo funciona la probabilidad: cuando se tira un dado de seis caras, la probabilidad de obtener cualquier número es de aproximadamente el 16,66 %. Si tira el dado 100 veces, es posible que no obtenga una distribución uniforme de aproximadamente 16 resultados para cada número. Sin embargo, cuantos más tiros realice, mayores serán sus posibilidades de obtener esa distribución uniforme. Tirar el dado 100.000 veces tendrá una mayor probabilidad de acercarse a esa división uniforme del 16,66 %. Esto es similar a por qué el aprendizaje de conjuntos es tan efectivo: más modelos pueden conducir a mejores resultados. -
Bosque aleatorio
No todos los métodos de conjunto agregan un conjunto diverso de modelos de entrenamiento. En realidad, algunos agregan varios modelos que usan el mismo algoritmo: la única diferencia es que cada modelo se entrena en un subconjunto diferente de los datos. El método de conjunto genera estos subconjuntos mediante un muestreo aleatorio de los datos de entrenamiento generales para cada modelo.
Un bosque aleatorio es un método de conjunto que agrega varios modelos de árbol de decisión y, en una tarea de clasificación, selecciona el modo de los clasificadores entre todos los árboles de decisión.
Figura 1. Un bosque aleatorio que selecciona un clasificador en función del modo de sus árboles constituyentes. Tenga en cuenta que el óvalo verde indica la clase 1 y los óvalos rojos indican la clase 0. 
En otras palabras, la clasificación que obtiene la mayor cantidad de votos entre todos los árboles de decisión es la clasificación que genera el bosque aleatorio. Al igual que con otros métodos de conjunto, esto normalmente resulta en una clasificación más hábil que si hubiera construido un solo árbol y utilizado sus resultados, o construido varios árboles y simplemente elegido el que tiene la mayor precisión. Otra forma de pensar en esto es que un bosque aleatorio reduce la tendencia de un solo modelo a sobreajustar a los datos de entrenamiento porque el bosque presenta niveles más bajos de varianza.
La mayoría de los bosques aleatorios utilizan una técnica de muestreo de datos llamada agregación de bootstrap, más comúnmente acortada a embolsado. Esta técnica muestrea el conjunto de datos de entrenamiento para cada árbol individual, con reemplazo. “Con reemplazo” significa que un ejemplo de datos puede aparecer en varios modelos diferentes. El embolsado tiende a conducir a una menor varianza, lo que reduce aún más el sobreajuste.
Nota: Los bosques aleatorios, al igual que otros algoritmos basados en árboles, no requieren que las características se escale para el entrenamiento.
Información adicional
Para obtener más información sobre los bosques aleatorios, consulte este sitio. -
Aumento de gradiente
Otro método de conjunto que incorpora varios árboles de decisión se denomina aumento de gradiente. Los algoritmos de aumento de gradiente crean modelos en etapas, donde los árboles de decisión pasados influyen en cómo se construyen los árboles de decisión posteriores. Esto los diferencia de los bosques aleatorios, donde cada árbol se construye de forma independiente y luego se muestrea aleatoriamente, lo que concluye en el voto mayoritario. Con el aumento del gradiente, los árboles se construyen de manera aditiva, donde cada árbol intenta corregir los errores del árbol anterior. Eso significa que sus conclusiones se desarrollan de forma iterativa, en lugar de determinarse de una sola vez. El algoritmo comienza generando árboles de decisión que tienen baja habilidad de clasificación (llamados aprendices débiles) y luego combina a esos aprendices débiles en un árbol de decisión eventual con alta habilidad de clasificación (llamado aprendiz fuerte).
Los modelos de aumento de gradiente pueden conducir a un mejor rendimiento en comparación con los bosques aleatorios, especialmente para conjuntos de datos desequilibrados. Sin embargo, son altamente susceptibles al sobreajuste en los casos en que los datos son ruidosos, y también pueden tardar más en entrenarse que los bosques aleatorios, ya que los árboles se construyen de forma iterativa en lugar de independiente. Los modelos de aumento de gradiente también son difíciles de ajustar. En términos de aplicaciones del mundo real, el aumento de gradiente ha tenido éxito en tareas como la clasificación de páginas para buscadores, la evaluación de riesgos en tiempo real y el análisis de datos científicos.
Información adicional
Para obtener más información sobre el aumento de gradiente, consulte este sitio. -
Entrenamiento y ajuste de modelos de árboles de decisión
Antes de empezar
Classification-Boston.ipynb está abierto en Jupyter Notebook.
Nota: Si cerró Jupyter Notebook desde que completó la actividad anterior, deberá reiniciar Jupyter Notebook y volver a abrir el archivo. Para asegurarse de que todos los objetos y la salida de Python están en el estado correcto para comenzar esta actividad:
1. Seleccione Kernel→Reiniciar & y Borrar salida.
2. Seleccione Reiniciar y borrar todas las salidas.
3. Desplácese hacia abajo y seleccione la celda con la etiqueta Crear un árbol de decisiones básico.
4. Seleccione Celda→ Ejecutar todo lo anterior.
Escenario
Finalizará el entrenamiento de los modelos de clasificación del Titanic creando un modelo de árbol de decisión solitario, así como un modelo de bosque aleatorio que agregue varios árboles. Los resultados de estos modelos pueden superar el rendimiento de los modelos de regresión logística y
k-NN que creó anteriormente.-------------------------------------------------------------------------------------------------------------------------------------------------------------
1.Cree un modelo básico de árbol de decisión.
1. Desplácese hacia abajo y vea la celda titulada Crear un modelo básico de árbol de decisión y examine la lista de código que aparece debajo de ella.

La línea 3 crea la versión scikit-learn del algoritmo CART para un árbol de decisión. El único hiperparámetro especificado es
random_state, que simplemente garantiza que los resultados sean los mismos cada vez que se ejecuta el código. De lo contrario, dado que no se especifica ningún otro hiperparámetro, el algoritmo utilizará los valores predeterminados:- criterionse establece comoginide forma predeterminada, que es el índice Gini utilizado por CART.- max_depthse establece comoNonede forma predeterminada; el árbol seguirá dividiéndose hasta que el índice de Gini sea 0 o hasta que todas las hojas contengan menos que número de muestras especificado pormin_samples_split.- min_samples_splitse establece como2de forma predeterminada.- min_samples_leafse establece como1de forma predeterminada.2. Ejecute la celda de código.3. Examine el resultado.

El modelo predeterminado tiene una precisión del 79 %.
4. En la siguiente celda de código, examine el código.

Este código utilizará el de árbol de decisiones para predecir la supervivencia de los pasajeros.
5. Ejecute la celda de código.
6. Examine el resultado.

Como es de esperar, los resultados de este modelo son diferentes de los resultados de los demás modelos.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------2. Ajuste un modelo básico de árbol de decisión.1. Desplácese hacia abajo y vea la celda titulada Ajustar un modelo básico de árbol de decisión y examine la lista de código que aparece debajo de ella.

Este código volverá a crear el modelo de árbol de decisiones básico, con un cambio en los hiperparámetros:
- max_depthahora se define explícitamente como6. Por lo tanto, el árbol no seguirá dividiéndose más allá de una profundidad de 6 ramas.2. Ejecute la celda de código.
3. Examine el resultado.

La puntuación de este modelo mejoró del 79 % al 83 % después del ajuste.
4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo de árbol de decisiones ajustado para predecir la supervivencia de los pasajeros en el conjunto de validación.
5. Ejecute la celda de código.
6. Examine el resultado.

Una vez más, los resultados ajustados difieren del original.
-------------------------------------------------------------------------------------------------------------------------------------------------------------3. Visualice el árbol de decisiones.
Desplácese hacia abajo y vea la celda titulada Visualizar el árbol de decisiones y examine la lista de código debajo de ella.

Este código creará una visualización del árbol de decisiones. La profundidad máxima se establece en 3 para limitar el tamaño de la visualización.
2. Ejecute la celda de código.
3. Examine el resultado.

Esta visualización trunca el árbol a una profundidad de tres. Cada nodo incluye información de división/decisión en ese nodo. Si hubiera impreso todo el árbol, podría continuar descendiendo por el árbol hasta llegar a la parte inferior, donde hay varias hojas, cada una con sus propias predicciones de clase basadas en la lógica de bifurcación de sus nodos primarios.
Este árbol comienza evaluando la característica
SexEncodingdel usuario. Recuerde que las pasajeras están codificadas como 1 y los pasajeros masculinos como 2. Por lo tanto, el nodo raíz evalúa si el valor codificado del pasajero es menor o igual que 1,5. Si es así, entonces esto significa que el pasajero es femenino. Si no, entonces el pasajero es masculino. En este punto del árbol, la decisión es que el pasajero pereció, simplemente porque más personas perecieron que sobrevivieron.Si el pasajero es mujer, continúa a lo largo del lado izquierdo del árbol hasta el siguiente nodo de decisión. Este nodo intenta determinar si la pasajera estaba o no en clase 2 o inferior. También predice la supervivencia. Las divisiones luego continúan para la edad y el tamaño de la familia del pasajero, cada uno de los cuales también predice la supervivencia. La división de edad termina en una predicción de supervivencia si la edad del pasajero era menor o igual a dos años, aunque continúa dividiéndose en función de la tarifa del boleto para cualquier pasajera que no fuera tan joven. El tamaño de la división familiar continúa por edad y tarifa de boleto.
En el lado derecho del árbol, se evalúa a los pasajeros masculinos. El nodo después del nodo raíz también comprueba la clase del pasajero, pero esta vez busca ver si el pasajero estaba en la clase 1. Los siguientes nodos de decisión comprueban la tarifa y la edad del pasajero. Las tarifas de boletos más bajas terminan en una predicción de "pereció", mientras que los valores más altos continúan dividiéndose en la tarifa. En cuanto a la rama de edad en el extremo derecho, la división continúa con el tamaño de la familia del pasajero para los pasajeros masculinos muy jóvenes, mientras que los pasajeros masculinos no tan jóvenes se continúan dividiendo según un valor de edad diferente.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------4. Cree un modelo de bosque aleatorio.
1. Desplácese hacia abajo y vea la celda titulada Crear un modelo de bosque aleatorio y examine la lista de código que aparece debajo de ella.

La implementación de bosque aleatorio en scikit-learn utiliza gran parte de los mismos hiperparámetros que un árbol de decisión solitario. Sin embargo, hay dos nuevos hiperparámetros:
- n_estimatorsespecifica cuántos árboles de decisión se crearán en el bosque. Tener más de unos pocos cientos de árboles por lo general solo hará que el proceso de entrenamiento sea más lento sin proporcionar ninguna ganancia significativa, por lo que 100 debería ser un número adecuado.- bootstrapespecifica si se realizará o no el embolsado.True, el valor predeterminado, significa que existirá. Si esFalse, todo el conjunto de entrenamiento se utilizará para cada árbol.2. Ejecute la celda de código.
3. Examine el resultado.

Este modelo de bosque aleatorio inicial tiene una precisión del 84 %.
4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo de bosque aleatorio para predecir la supervivencia de los pasajeros.
5. Ejecute la celda de código.
6. Examine el resultado.

-------------------------------------------------------------------------------------------------------------------------------------------------------------
5. Ajuste un modelo de bosque aleatorio.
1. Desplácese hacia abajo y vea la celda titulada Ajustar un modelo de bosque aleatorio y examine la lista de código que aparece debajo de ella.

Este código volverá a crear el modelo de bosque aleatorio utilizando valores de hiperparámetro diferentes.
- El valor del hiperparámetro
n_estimatorsse cambió de100a150.- El valor del hiperparámetro
max_depthse cambió de6a10.- El valor del hiperparámetro
min_samples_leafse cambió de10a12.2. Ejecute la celda de código.
3. Examine el resultado.

La puntuación de este modelo tuvo una leve mejora del 84 % al 85 % después del ajuste.
4. En la siguiente celda de código, examine el código.

Este código utilizará el modelo de bosque aleatorio ajustado para predecir la supervivencia de los pasajeros en el conjunto de validación.
5. Ejecute la celda de código.
6. Examine el resultado.

------------------------------------------------------------------------------------------------------------------------------------------------------------------------6. Visualice la estructura de un árbol de decisiones en el bosque.
1. Desplácese hacia abajo y vea la celda titulada Visualizar la estructura de un árbol de decisiones en el bosque y examine la lista de código debajo de ella.
Este código creará una visualización del primer árbol del bosque.
2. Ejecute la celda de código.
3. Examine el resultado.

Este árbol comienza evaluando
SexEncodingcomo lo hizo con el árbol de decisión solitario anteriormente. Sin embargo, los nodos de decisión se dividen en diferentes características. Por ejemplo, el primer nodo de decisión para las pasajeras femeninas se divide enParch(número de padres más hijos que el pasajero tenía a bordo), mientras que el primer nodo de decisión para los pasajeros masculinos se divide en el título del pasajero.Recuerde que hay otros 99 árboles en este bosque. Cada árbol entrena en un muestreo diferente de los datos generales, por lo que es probable que cada árbol tome diferentes decisiones de división.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------7. Observe otro árbol en el bosque.1. Desplácese hacia abajo y vea la celda titulada Observar otro árbol en el bosque y examine la lista de código debajo de ella.

Este código creará una visualización del segundo árbol del bosque.
2. Ejecute la celda de código.
3. Examine el resultado.

Este árbol es diferente al primero. Comienza a dividirse según la clase del pasajero en lugar de
SexEncoding. Cualquier persona en primera clase se mueve por el lado izquierdo del árbol en una decisión de división basada en su título. Cualquier persona que no esté en la primera clase viaja por el lado derecho del árbol, donde se evalúa como hombre o mujer. Como antes, el árbol continúa tomando decisiones de división después de esto.Como se muestra aquí, no todos los árboles de un bosque seguirán la misma lógica de división. Esto es, en última instancia, algo bueno, ya que el propósito de un bosque aleatorio es construir consenso a partir de las predicciones de clase de cada árbol, en lugar de simplemente generar los mismos árboles una y otra vez.
-

